某校高三年级一次数学考试之后,为了解学生的数学学习情况, 随机抽取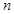
名学生的数学成绩, 制成下表所示的频率分布表．
(1)求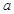
，
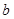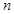，的值;
(2)若从第三, 四, 五组中用分层抽样方法抽取6名学生，并在这6名学生中随机抽取2名与张老师面谈，求第三组中至少有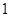
名学生与张老师面谈的概率．
| 组号 |
分组 |
频数 |
频率 |
| 第一组 |
 |
 |
 |
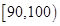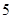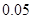| 第二组 |
 |
|
 |
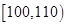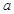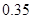| 第三组 |
 |
 |
 |
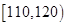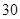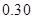| 第四组 |
 |
 |
|
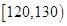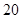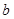| 第五组 |
 |
 |
 |
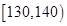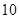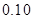| 合计 |
|
 |
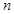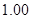(本小题满分14分)
已知向量a =" (" sinx , 0 ), b =" (cosx," 1), 其中 0 < x <
, 求|
a –
b |的取值范围
(本小题满分14分)
设Sn是首项为4, 公差d ¹ 0的等差数列{a n}的前n项和，若
S3和
S4的等比中项为
S5. 求：:
(1) {an}的通项公式an;
(2) 使Sn> 0的最大n值
(本小题满分14分)
解不等式log3(x2 – 6x + 8 ) – log3x < 1
(本小题满分14分)
已知a、b、c是△ABC中A、B、C的对边, 关于x的方程b (x 2 + 1 ) + c (x 2– 1 ) –2ax =" 0" 有两个相等的实根, 且sinCcosA – cosCsinA="0," 试判定△ABC的形状.
（本小题满分10分）选修4-5：不等式选讲
已知函数
.
（Ⅰ）解不等式
≤4；（Ⅱ）若存在x使得
≤0成立，求实数a的取值范围.