已知无穷数列 中,
中,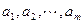 是首项为
是首项为 ,公差为
,公差为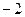 的等差数列;
的等差数列; 是首项为
是首项为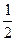 ,公比为
,公比为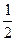 的等比数列
的等比数列 ,并对任意
,并对任意 ,均有
,均有 成立,(1)当
成立,(1)当 时,求
时,求 ; (2)若
; (2)若 ,试求
,试求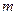 的值;(3)判断是否存在
的值;(3)判断是否存在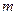 ,使
,使 成立,若存在,求出
成立,若存在,求出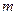 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
已知在等差数列{ }中,
}中, =3,前7项和
=3,前7项和 =28.
=28.
(I)求数列{ }的公差d;
}的公差d;
(II)若数列{ }为等比数列,且
}为等比数列,且 ,
, 求数列
求数列 的前n项和
的前n项和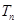
 .
.
设正有理数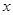 是
是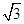 的一个近似值,令
的一个近似值,令 .
.
(Ⅰ)若 ,求证:
,求证: ;
;
(Ⅱ)比较 与
与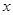 哪一个更接近
哪一个更接近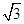 ,请说明理由.
,请说明理由.
在直角坐标系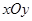 中,已知圆
中,已知圆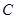 的参数方程
的参数方程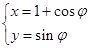 (
(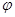 为参数),以
为参数),以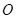 为极点,
为极点,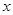 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(Ⅰ)求圆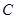 的极坐标方程;
的极坐标方程;
(Ⅱ)直线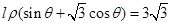 ,射线
,射线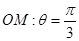 与圆
与圆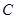 的交点为
的交点为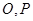 ,与直线
,与直线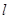 的交点为
的交点为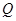 ,求线段
,求线段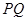 的长.
的长.
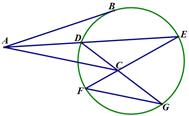
切线 与圆切于点
与圆切于点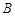 ,圆内有一点
,圆内有一点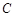 满足
满足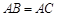 ,
,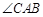 的平分线
的平分线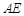 交圆于
交圆于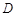 ,
,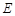 ,延长
,延长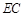 交圆于
交圆于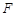 ,延长
,延长 交圆于
交圆于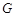 ,连接
,连接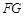 .
.
(Ⅰ)证明: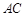 //
//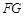 ;
;
(Ⅱ)求证: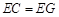 .
.
已知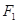 ,
,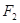 分别是椭圆
分别是椭圆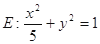 的左、右焦点
的左、右焦点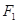 ,
,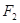 关于直线
关于直线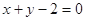 的对称点是圆
的对称点是圆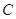 的一条直径的两个端点.
的一条直径的两个端点.
(Ⅰ)求圆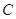 的方程;
的方程;
(Ⅱ)设过点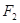 的直线
的直线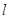 被椭圆
被椭圆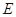 和圆
和圆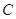 所截得的弦长分别为
所截得的弦长分别为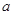 ,
,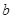 .当
.当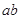 最大时,求直线
最大时,求直线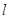 的方程.
的方程.