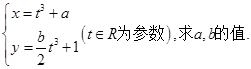(本小题满分12分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四张卡片,现从甲、乙两个盒子中各取出1张卡片,每张卡片被取出的可能性相等;
(Ⅰ)求取出的两张卡片标号之积能被3整除的概率;
(Ⅱ)如果小王、小李取出的两张卡片的标号相加,谁的两张卡片标号之和大则谁胜出,若小王先抽,抽出卡片的标号分别为3和4,且小王抽出的两张卡片不再放回盒中,小李再抽;求小王胜出的概率。
在平面直角坐标系中,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.已知直线l上两点M,N的极坐标分别为(2,0),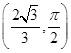 ,圆C的参数方程为
,圆C的参数方程为 (θ为参数).
(θ为参数).
(1)设P为线段MN的中点,求直线OP的平面直角坐标方程;
(2)判断直线l与圆C的位置关系.
在极坐标系中,已知圆C经过点P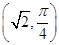 ,圆心为直线ρsin
,圆心为直线ρsin =-
=-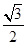 与极轴的交点,求圆C的极坐标方程.
与极轴的交点,求圆C的极坐标方程.
已知曲线C1的参数方程是 (φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为
(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2,正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为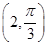 .
.
(1)求点A,B,C,D的直角坐标;
(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.
在直角坐标系xOy.圆C1:x2+y2=4,圆C2:(x-2)2+y2=4.
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2的交点坐标(用极坐标表示);
(2)求圆C1与C2的公共弦的参数方程.
在直角坐标系 中以
中以 为极点,
为极点, 轴正半轴为极轴建立坐标系.圆
轴正半轴为极轴建立坐标系.圆 ,直线
,直线 的极坐标方程分别为
的极坐标方程分别为 .
.
(1)
(2)