“天宫一号”的顺利升空标志着我国火箭运载的技术日趋完善.据悉,担任“天宫一号”发射任务的是长征二号FT1火箭.为了确保发射万无一失,科学家对长征二号FT1运载火箭进行了170余项技术状态更改,增加了某项新技术.该项新技术要进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测.假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响.
(I)求该项技术量化得分不低于8分的概率;
(II)记该项技术的三个指标中被检测合格的指标个数为随机变量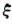 ,求
,求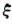 的分布列与数学期望
的分布列与数学期望
如图,在四棱锥P—ABCD中,底面ABCD是边长为4的菱形,且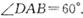 菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
菱形ABCD的两条对角线的交点为O,PA=PC,PB=PD且PO= 3.点E是线段PA的中点,连接EO,EB,EC
(I)证明:直线0E//平面PBC;
(II)求二面角E-BC-D的大小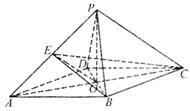
已知 中,内角A、B、C所对边的长分别是a、b、c,且点
中,内角A、B、C所对边的长分别是a、b、c,且点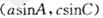 在直线
在直线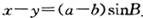 上.
上.
(I)求角C的大小;
(II)若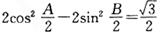 ,且A<B,求.
,且A<B,求.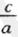 的值.
的值.
甲乙两物体分别从相距70米的两处同时运动,甲第一分钟走2米,以后每分钟比前一分钟多走1米,乙每分钟走5米。
(1).甲乙开始运动后几分钟相遇?
(2)如果.甲乙到达对方起点后立即折返,甲继续每分钟比前一分钟多走1米,乙继续每分钟走5米,那么开始运动几分钟后第二次相遇。
已知函数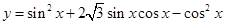 ,
,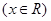
(1)求最小正周期(2)单调增区间
(3)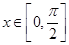 时,求函数的值域。
时,求函数的值域。