如图所示,倾斜角为 的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
的直线经过抛物线y2=8x的焦点F,且与抛物线交于A、B两点.
(1)求抛物线焦点F的坐标及准线l的方程;
(2)若 为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2
为锐角,作线段AB的垂直平分线m交x轴于点P,证明|FP|-|FP|cos2 为定值,
为定值,
并求此定值.
(本小题满分12分)
袋中装着标有数字1,2,3,4的小球各3个,从袋中任取3个小球,每个小球被取出的可能性都相等.
(Ⅰ)求取出的3个小球上的数字互不相同的概率;
(Ⅱ)用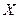 表示取出的3个小球上所标的最大数字,求随机变量
表示取出的3个小球上所标的最大数字,求随机变量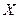 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
已知坐标平面上三点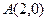 ,
, ,
,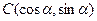 .
.
(1)若 (O为坐标原点),求向量
(O为坐标原点),求向量 与
与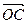 夹角的大小;
夹角的大小;
(2)若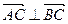 ,求
,求 的值.
的值.
(本小题满分14分)
已知数列{an}中,a1="1" ,a2=3,且点(n,an)满足函数y = kx + b.
(1)求k,b的值,并写出数列{an}的通项公式;
(2)记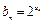 ,求数列{bn}的前n和Sn.
,求数列{bn}的前n和Sn.
(本小题满分12分)
设函数 ,其中向量
,其中向量 ,
, ,
, ,且
,且 的图象经过点
的图象经过点 .(1)求实数
.(1)求实数 的值;
的值;
(2)求函数 的最小值及此时
的最小值及此时 值的集合.
值的集合.
(本小题满分12分)
不等式mx2-mx+1>0,对任意实数x都成立,求m的取值范围。