在墙上挂着一块边长为16cm的正方形木板,上面画了大、中、小三个同心圆,半径分别为2cm、4cm、6cm,某人站在3m之外向此板投镖,设投中线上或没有投中木板时不算,可重投,问:
(1)投中大圆内的概率是多少?
(2)投中小圆与中圆形成的圆环的概率是多少?
(3)投中大圆之外的概率是多少?
已知 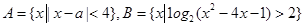
(1)若 =l,求
=l,求 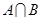 ;
;
(2)若 ,求实数
,求实数 的取值范围.
的取值范围.
已知抛物线 的焦点为
的焦点为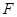 ,过
,过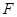 任作直线
任作直线 (
( 与
与 轴不平行)交抛物线分别于
轴不平行)交抛物线分别于 两点,点
两点,点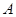 关于
关于 轴对称点为
轴对称点为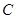 ,
,
(1)求证:直线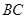 与
与 轴交点
轴交点 必为定点;
必为定点;
(2)过 分别作抛物线的切线,两条切线交于
分别作抛物线的切线,两条切线交于 ,求
,求 的最小值,并求当
的最小值,并求当 取最小值时直线
取最小值时直线 的方程.
的方程.
已知函数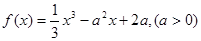
(1)求函数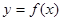 的单调区间;
的单调区间;
(2)若在区间[0,2]上恒有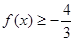 ,求
,求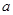 的取值范围.
的取值范围.
已知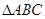 中,
中,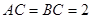 ,
,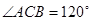 ,
,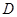 为
为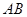 的中点,
的中点,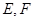 分别在线段
分别在线段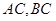 上,且
上,且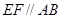
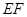 交
交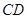 于
于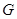 ,把
,把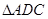 沿
沿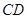 折起,如下图所示,
折起,如下图所示,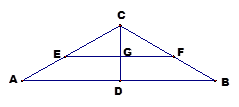
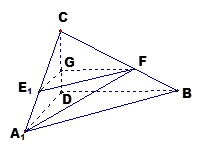
(1)求证: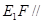 平面
平面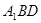 ;
;
(2)当二面角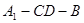 为直二面角时,是否存在点
为直二面角时,是否存在点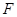 ,使得直线
,使得直线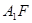 与平面
与平面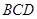 所成的角为
所成的角为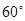 ,若存在求
,若存在求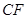 的长,若不存在说明理由.
的长,若不存在说明理由.
已知等比数列 中,
中, 且
且 ,
, ,
, 成等差数列,
成等差数列,
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项的和.
项的和.