设人的某一特征(如眼睛大小)是由他的一对基因所决定的,以x表示显性基因,y表示隐性基因,则具有xx基因的人为纯显性,具有yy基因的人是纯隐性。纯显性与混合性的人都有显露显性基因决定的某一特征,孩子从父母身上各得到1个基因。假定父母都是混合性,问:
(1)1个孩子由显性基因决定的特征的概率是多少?
(2)2个孩子中至少有一个显性基因决定的特征的概率是多少?
设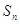 为数列{
为数列{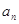 }的前项和,已知
}的前项和,已知 ,2
,2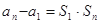 ,
, N
N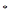
(1)求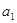 ,并求数列{
,并求数列{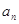 }的通项公式;(2)求数列{
}的通项公式;(2)求数列{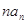 }的前
}的前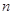 项和.
项和.
如图,在边长为1的等边三角形 中,
中, 分别是
分别是 边上的点,
边上的点,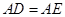 ,
,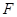 是
是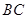 的中点,
的中点, 与
与 交于点
交于点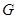 ,将
,将 沿
沿 折起,得到如图5所示的三棱锥
折起,得到如图5所示的三棱锥 ,其中
,其中 .
.
(1) 证明: //平面
//平面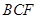 ;
;
(2) 证明:
 平面
平面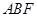 ;
;
(3) 当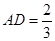 时,求三棱锥
时,求三棱锥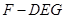 的体积
的体积 .
.
已知函数 ,
, .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 .
.
(1) 的方程为
的方程为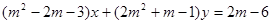 ,根据下列条件分别确定
,根据下列条件分别确定 的值.①
的值.① 轴上的截距是
轴上的截距是 ;②
;② 的倾斜角为
的倾斜角为 ;
;
(2)求经过直线 ,
,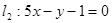 的交点,并且与直线
的交点,并且与直线 垂直的直线方程
垂直的直线方程
已知数列 的前
的前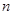 项和为
项和为 ,且
,且 ,设
,设 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)求数列 的前
的前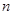 项和
项和 ;
;
(3)设 ,
, ,若数列
,若数列 的前
的前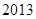 项和为
项和为 ,求不超过
,求不超过 的最大的整数值.
的最大的整数值.