(1)4名同学选报跑步、跳高、跳远三个项目,每人报一项,共有多少种报名方法?
(2)4名同学争夺跑步、跳高、跳远三项冠军,共有多少种可能的结果?
(本小题12分)
随机抽取某中学甲乙两个班级各10名同学,测量他们的身高(单位:cm),获得的数据如下:
甲:182 170 171 179 179 162 163 168 168 158
乙:181 170 173 176 178 179 162 165 168 159
(1)根据上述的数据作出茎叶图表示;
(2)判断哪个班级的平均身高较高,并求出甲班的方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,身高176cm的同学被抽中的概率是多少?
(本小题12分)
已知四棱台 的三视图如图所示,
的三视图如图所示,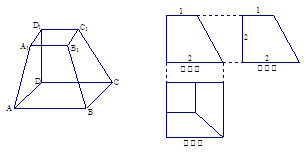
(1)求证: 平面
平面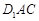 ;
;
(2)求证:平面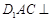 平面
平面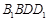 ;
;
(3)求此四棱台 的体积.
的体积.
(本小题12分)
已知数列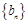 的前
的前 项和为
项和为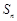 ,
, 且
且
(1)求数列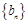 的通项公式;
的通项公式;
(2)求数列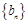 的前
的前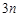 项的和.
项的和.
(本小题满分14分)在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东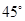 且与点A相距40
且与点A相距40 海里的位置B,经过40分钟又测得该船已行驶到点A北偏东
海里的位置B,经过40分钟又测得该船已行驶到点A北偏东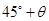 (其中
(其中 ,
,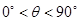 )且与点A相距10
)且与点A相距10 海里的位置C.
海里的位置C.
(1)求该船的行驶速度(单位:海里/小时);
(2)若该船不改变航行方向继续行驶.判断它是否会进入警戒水域,并说明理由
(本小题满分14分)设函数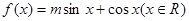 的图象经过点
的图象经过点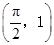 .
.
(1)求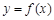 的解析式,并求函数的最小正周期和最大值.
的解析式,并求函数的最小正周期和最大值.
(2)若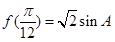 ,其中
,其中 是面积为
是面积为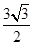 的锐角
的锐角 的内角,且
的内角,且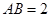 ,
,
求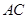 和
和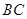 的长.
的长.