(本小题12分)
随机抽取某中学甲乙两个班级各10名同学,测量他们的身高(单位:cm),获得的数据如下:
甲:182 170 171 179 179 162 163 168 168 158
乙:181 170 173 176 178 179 162 165 168 159
(1)根据上述的数据作出茎叶图表示;
(2)判断哪个班级的平均身高较高,并求出甲班的方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,身高176cm的同学被抽中的概率是多少?
如图,在四棱锥P-ABCD中,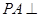 平面ABCD,AD//BC,
平面ABCD,AD//BC,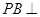 AC,
AC,
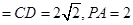 ,点M在线段PD上.
,点M在线段PD上.
(1)求证: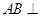 平面PAC;
平面PAC;
(2)若二面角M-AC-D的大小为 ,试确定点M的位置.
,试确定点M的位置.
某学校组织了一次安全知识竞赛,现随机抽取20名学生的测试成绩,如下表所示(不低于90分的测试成绩称为“优秀成绩”):
| 79 |
90 |
82 |
80 |
84 |
95 |
79 |
86 |
89 |
91 |
| 97 |
86 |
79 |
78 |
86 |
77 |
87 |
89 |
83 |
85 |
(1)若从这20人中随机选取3人,求至多有1人是“优秀成绩”的概率;
(2)以这20人的样本数据来估计整个学校的总体数据,若从该校全体学生中(人数很多)任选3人,记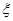 表示抽到“优秀成绩”学生的人数,求
表示抽到“优秀成绩”学生的人数,求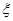 的分布列及数学期望.
的分布列及数学期望.
在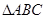 中,角A,B,C的对边分别为a,b,c,若
中,角A,B,C的对边分别为a,b,c,若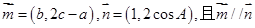 .
.
(1)求B;
(2)设函数 ,求函数
,求函数 上的取值范围.
上的取值范围.
在无穷数列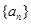 中,
中,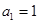 ,对于任意
,对于任意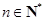 ,都有
,都有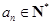 ,
,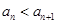 . 设
. 设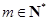 , 记使得
, 记使得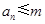 成立的
成立的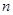 的最大值为
的最大值为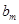 .
.
(1)设数列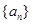 为1,3,5,7,
为1,3,5,7,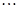 ,写出
,写出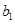 ,
,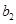 ,
,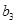 的值;
的值;
(2)若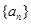 为等比数列,且
为等比数列,且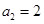 ,求
,求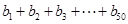 的值;
的值;
(3)若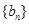 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列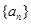 .
.
设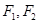 分别为椭圆
分别为椭圆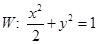 的左、右焦点,斜率为
的左、右焦点,斜率为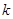 的直线
的直线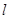 经过右焦点
经过右焦点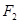 ,且与椭圆W相交于
,且与椭圆W相交于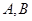 两点.
两点.
(1)求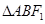 的周长;
的周长;
(2)如果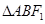 为直角三角形,求直线
为直角三角形,求直线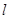 的斜率
的斜率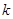 .
.