已知m∈R，复数z(m22m3)i,当m为何值时，（1）z∈-优题课

已知m∈R，复数z=+(m²+2m-3)i,当m为何值时，（1）z∈R；（2）z是纯虚数；（3）z对应的点位于复平面第二象限；（4）z对应的点在直线x+y+3=0上.

科目数学题型解答题难度较易

（本小题满分12分）
甲、乙两人进行一场乒乓球比赛，根据以往比赛的胜负情况知道，每一局比赛甲胜的概率0.6，乙胜的概率为0.4，本场比赛采用三局两胜制。
（1）求甲获胜的概率.
（2）设ξ为本场比赛的局数，求ξ的概率分布和数学期望.

（本小题满分12分）
已知函数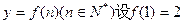，且任意的

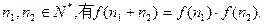
（1）求、、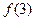的值；
（2）试猜想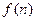的解析式，并用数学归纳法给出证明.

（本小题满分10分）
已知函数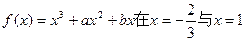处都取得极值.
（1）求a，b的值；
（2）求的单调区间及极大值、极小值

（本小题满分10分）
已知在（1－2log₂x）ⁿ的展开式中所有奇数项的二项式系数的和为64.
（1）求n的值；
（2）求展开式中所有项的系数之和.

如图， $△ A B C$ 的角平分线 $A D$ 的延长线交它的外接圆于点 $E$ .

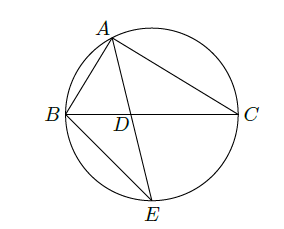
（Ⅰ）证明： $△ A B E ~ △ A D C$ ；
（Ⅱ）若 $△ A B C$ 的面积 $S = \frac{1}{2} A D \cdot A E$ ,求 $∠ B A C$ 的大小.