如图所示,在△ABO中, =
=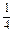
 ,
, =
=
 ,AD与BC相交于点M,设
,AD与BC相交于点M,设 =a,
=a, =b.试用a和b表示向量
=b.试用a和b表示向量 .
.
直线 l 被两直线 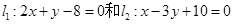 截得线段中点是M
截得线段中点是M
(0,1),求l方程。
已知函数f(x)=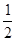 x
x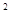 -ax+(a-1)
-ax+(a-1) ,
,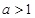 。
。
(1)讨论函数 的单调性;
的单调性;
(2)证明:若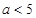 ,则对任意x
,则对任意x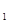 ,x
,x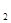
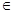
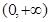 ,x
,x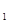
 x
x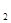 ,有
,有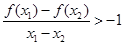 。
。
已知,椭圆C过点A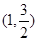 ,两个焦点为(-1,0),(1,0)。
,两个焦点为(-1,0),(1,0)。
(1)求椭圆C的方程;
(2)E、F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
在平面直角坐标系 中,已知圆
中,已知圆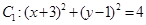 和圆
和圆 ,
,
(1)若直线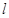 过点
过点 ,且被圆
,且被圆 截得的弦长为
截得的弦长为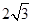 ,求直线
,求直线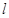 的方程;
的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线 和
和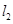 ,它们分别与
,它们分别与
圆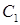 和圆
和圆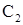 相交,且直线
相交,且直线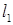 被圆
被圆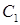 截得的弦长与直线
截得的弦长与直线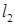 被圆
被圆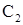 截得的弦长相等,试求所
截得的弦长相等,试求所
有满足条件的点P的坐标。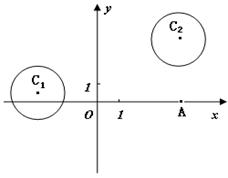
设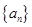 是公差不为零的等差数列,
是公差不为零的等差数列,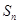 为其前
为其前 项和,满足
项和,满足 ,
,
(1)求数列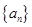 的通项公式及前
的通项公式及前 项和
项和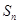 ;
;
(2)试求所有的正整数 ,使得
,使得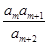 为数列
为数列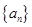 中的项。
中的项。