已知a、b、c是△ABC的三边长,关于x的方程ax2-2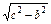 x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10
x-b="0" (a>c>b)的两根之差的平方等于4,△ABC的面积S=10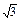 ,c=7.
,c=7.
(1)求角C;
(2)求a,b的值.
生产工艺工程中产品的尺寸偏差 ,如果产品的尺寸与现实的尺寸偏差的绝对值不超过4mm的为合格品,求生产5件产品的合格率不小于
,如果产品的尺寸与现实的尺寸偏差的绝对值不超过4mm的为合格品,求生产5件产品的合格率不小于 的概率.(精确到0.001).
的概率.(精确到0.001).
掷3枚均匀硬币一次,求正面个数与反面个数之差X的分布列,并求其均值和方差.
某一中学生心理咨询中心服务电话接通率为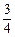 ,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.
,某班3名同学商定明天分别就同一问题询问服务中心,且每人只拨打一次,求他们中成功咨询的人数X的分布列.
如图,电路由电池 并联组成.电池
并联组成.电池 损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.
损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.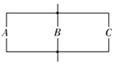
某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求这位射手在三次射击中命中目标的概率;
(2)求这位射手在这次射击比赛中得分的均值.