在△ABC中,设A、B、C的对边分别为a、b、c,向量m=(cosA,sinA),n=( -sinA,cosA),若|m+n|=2.
-sinA,cosA),若|m+n|=2.
(1)求角A的大小;
(2)若b=4 ,且c=
,且c= a,求△ABC的面积.
a,求△ABC的面积.
如图,已知二面角 的大小为
的大小为 ,菱形
,菱形 在面
在面 内,
内, 两点在棱
两点在棱 上,
上, ,
, 是
是 的中点,
的中点, 面
面 ,垂足为
,垂足为 .
.
(1)证明: 平面
平面 ;
;
(2)求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
如图,在三棱锥 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求二面角 的平面角的余弦值..
的平面角的余弦值..
已知圆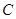 与两平行直线
与两平行直线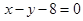 和
和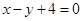 相切,圆心在直线
相切,圆心在直线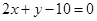 上.
上.
(1)求圆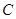 的方程;
的方程;
(2)过原点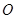 做一条直线,交圆
做一条直线,交圆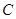 于
于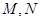 两点,求
两点,求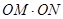 的值.
的值.
如图,长方体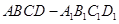 中,
中,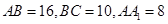 ,点
,点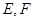 分别在
分别在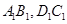 上,
上, ,过点
,过点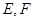 的平面
的平面 与此长方体的面相交,交线围成一个正方形.
与此长方体的面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法与理由).
(2)求平面 把该长方体分成的两部分体积的比值.
把该长方体分成的两部分体积的比值.
已知正方形ABCD的中心M(-1,0)和一边CD所在的直线方程为x+3y-5=0,求其他三边所在的直线方程.