求过两直线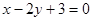 和
和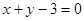 的交点,且满足下列条件的直线
的交点,且满足下列条件的直线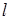 的方程.
的方程.
(Ⅰ)和直线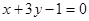 垂直;
垂直;
(Ⅱ)在 轴,
轴, 轴上的截距相等.
轴上的截距相等.
设函数 ,曲线
,曲线 在点(1,
在点(1,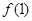 处的切线为
处的切线为 . (Ⅰ)求
. (Ⅰ)求 ;
;
(Ⅱ)证明: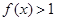 .
.
一走廊拐角处的横截面如图所示,已知内壁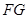 和外壁
和外壁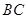 都是半径为1m的四分之一圆弧,
都是半径为1m的四分之一圆弧, 分别与圆弧
分别与圆弧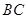 相切于
相切于 两点,
两点, 且两组平行墙壁间的走廊宽度都是1m.
且两组平行墙壁间的走廊宽度都是1m.
(1)若水平放置的木棒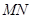 的两个端点
的两个端点 分别在外壁
分别在外壁 和
和 上,且木棒与内壁圆弧相切于点
上,且木棒与内壁圆弧相切于点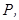 设
设 试用
试用 表示木棒
表示木棒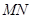 的长度
的长度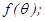
(2)若一根水平放置的木棒能通过该走廊拐角处,求木棒长度的最大值.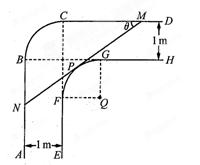
在 中,内角
中,内角 所对的边分别为
所对的边分别为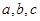 .已知
.已知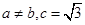 ,
,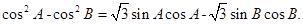
(1)求角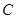 的大小;
的大小;
(2)若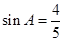 ,求
,求 的面积.
的面积.
已知命题 指数函数
指数函数 在
在 上单调递减,命题
上单调递减,命题 关于
关于 的方程
的方程
 的两个实根均大于3.若“
的两个实根均大于3.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知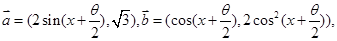 且
且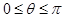 ,
,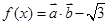 ,且
,且 为偶函数.
为偶函数.
(1)求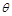 ;
;
(2)求满足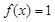 ,
, 的x的集合.
的x的集合.