正方形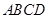
所在平面与平面四边形
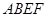所在平面互相垂直，△
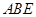是等腰直角三角形，
（1）求证：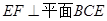
；
（2）设线段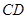
的中点为
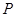，在直线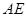
上是否存在一点
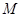，使得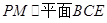
？若存在，请指出点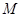的位置，并证明你的结论；若不存在，请说明理由；
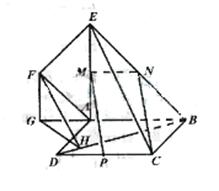
如图，△ABC中，AC＝BC＝
AB，ABED是边长为1的正方形，EB⊥底面ABC，若G，F分别是EC，BD的中点．
(1)求证：GF∥底面ABC；
(2)求证：AC⊥平面EBC；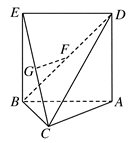
圆柱的高是8 cm，表面积是130 π cm2，求它的底面圆半径和体积．
已知数列
满足
（
）且
（1）求
的值
（2）求的通项公式
（3）令
，求
的最小值及此时
的值
某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为
层，则每平方米的平均建筑费用为
（单位：元）．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？
（注：平均综合费用
平均建筑费用
平均购地费用，平均购地费用
）
已知
是等差数列，且
（1）求数列的通项公式及前
项的和
（2）令
，求
的前项的和