设a= ,b=(4sinx,cosx-sinx),f(x)=a·b.
,b=(4sinx,cosx-sinx),f(x)=a·b.
(1)求函数f(x)的解析式;
(2)已知常数 >0,若y=f(
>0,若y=f( x)在区间
x)在区间 上是增函数,求
上是增函数,求 的取值范围;
的取值范围;
(3)设集合A= ,B={x||f(x)-m|<2},若A
,B={x||f(x)-m|<2},若A B,求实数m的取值范围.
B,求实数m的取值范围.
在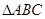 中,角
中,角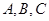 所对的边分别是
所对的边分别是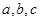 ,已知
,已知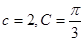 .
.
(Ⅰ)若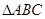 的面积等于
的面积等于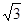 ,求
,求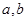 ;
;
(Ⅱ)若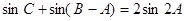 ,求
,求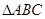 的面积.
的面积.
如图,已知椭圆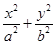 (a>b>0)的离心率
(a>b>0)的离心率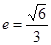 ,过点A(0,-b)和B(a,0)的直线与原点的距离为
,过点A(0,-b)和B(a,0)的直线与原点的距离为 .
.
(1)求椭圆的方程.
(2)已知定点E(-1,0),若直线y=kx+2(k≠0)与椭圆交于C、D两点.问:是否存在k的值,使以CD为直径的圆过E点?请说明理由.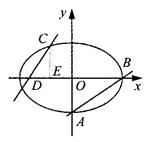
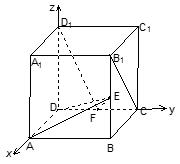
在正方体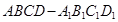 中,如图E、F分别是
中,如图E、F分别是 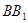 ,CD的中点,
,CD的中点,
(1)求证: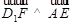 ;
;
(2)求 .
. 
已知:等差数列{ }中,
}中, =14,前10项和
=14,前10项和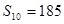 .
.
(Ⅰ)求 ;
;
(Ⅱ)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和 .
.
抛物线的顶点在原点,它的准线过双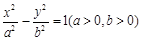 曲线的一个焦点,并与
曲线的一个焦点,并与
双曲线的实轴垂直,已知抛物线与双曲线的交点为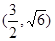 ,求抛物线的方程和双曲线的方程.
,求抛物线的方程和双曲线的方程.