已知:等差数列{ }中,
}中, =14,前10项和
=14,前10项和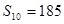 .
.
(Ⅰ)求 ;
;
(Ⅱ)将{ }中的第2项,第4项,…,第
}中的第2项,第4项,…,第 项按原来的顺序排成一个新数列,求此数列的前
项按原来的顺序排成一个新数列,求此数列的前 项和
项和 .
.
(本题满分14分)如图,正方形ABCD和四边形ACEF所在的平面互相垂直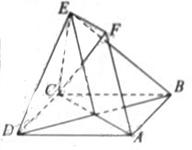
EF//AC,AB= ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE
(Ⅱ)求证:CF⊥平面BDE;

在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点.已知|AB|=2|OA|,且点B的纵坐标大于零.
(1)求向量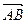 的坐标;
的坐标;
(2)求圆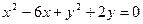 关于直线OB对称的圆的方程;
关于直线OB对称的圆的方程;
(3)是否存在实数a,使函数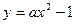 的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个点?若不存在,说明理由:若存在,求a的取值范围.
设有关于x的一元二次方程x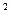 -2ax+b
-2ax+b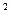 =0
=0
(1)若a是从0、1、2、3四个数中任取的一个数,b是从0、1、2三个数中任取的一个数,求上述方程没有实根的概率
(2))若a是从区间 [0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程没有实根的
[0,3]内任取的一个数,b是从区间[0,2]内任取的一个数,求上述方程没有实根的 概率
概率