(本题满分14分)如图,正方形ABCD和四边形ACEF所在的平面互相垂直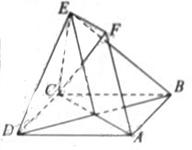
EF//AC,AB= ,CE=EF=1
,CE=EF=1
(Ⅰ)求证:AF//平面BDE
(Ⅱ)求证:CF⊥平面BDE;
如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
如右图所示,在三棱锥A-BCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.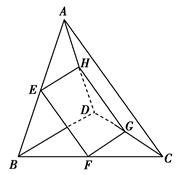
(1)求证:四边形EFGH是平行四边形;
(2)若AC=BD,求证:四边形EFGH是菱形;
(3)当AC与BD满足什么条件时,四边形EFGH是正方形
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.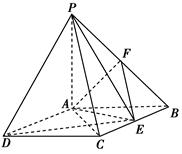
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.
如右图所示,ABCD-A1B1C1D1是正四棱柱,侧棱长为1,底面边长为2,E是棱BC的中点.
(1)求证:BD1∥平面C1DE;
(2)求三棱锥D-D1BC的体积
一几何体的表面展开图如右图,则这个几何体是哪一种几何体?选择适当的角度,画出它水平放置时的直观图与三视图.并计算该几何体的体积.