(本小题满分12分)
四个大小相同的小球分别标有数字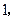
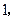
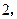
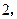 把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为
把它们放在一个盒子中,从中任意摸出两个小球,它们的标号分别为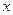 、
、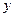 ,记随机变量
,记随机变量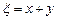 .
.
(1)求随机变量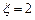 时的概率;
时的概率;
(2)求随机变量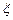 的概率分布列及数学期望。
的概率分布列及数学期望。
已知函数 ,设数列
,设数列 满足:
满足: ,
, .
.
(1)求证: ,都有
,都有 ;
;
(2)求证:
某商场举办“迎新年摸球”活动,主办方准备了甲、乙两个箱子,其中甲箱中有四个球,乙箱中有三个球(每个球的大小、形状完全相同),每一个箱子中只有一个红球,其余都是黑球. 若摸中甲箱中的红球,则可获奖金 元,若摸中乙箱中的红球,则可获奖金
元,若摸中乙箱中的红球,则可获奖金 元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
(1)如果参与者先在乙箱中摸球,求其恰好获得奖金 元的概率;
元的概率;
(2)若要使得该参与者获奖金额的期望值较大,请你帮他设计摸箱子的顺序,并说明理由.
在极坐标系中,求圆 上的点到直线
上的点到直线 (
( )距离的最大值.
)距离的最大值.
已知直线 在矩阵
在矩阵 对应的变换作用下变为直线
对应的变换作用下变为直线 ,求矩阵
,求矩阵 .
.
若数列 中不超过
中不超过 的项数恰为
的项数恰为 (
( ),则称数列
),则称数列 是数列
是数列 的生成数列,称相应的函数
的生成数列,称相应的函数 是数列
是数列 生成
生成 的控制函数.
的控制函数.
(1)已知 ,且
,且 ,写出
,写出 、
、 、
、 ;
;
(2)已知 ,且
,且 ,求
,求 的前
的前 项和
项和 ;
;
(3)已知 ,且
,且 (
( ),若数列
),若数列 中,
中, ,
, ,
, 是公差为
是公差为 (
( )的等差数列,且
)的等差数列,且 ,求
,求 的值及
的值及 的值
的值