某商场举办“迎新年摸球”活动,主办方准备了甲、乙两个箱子,其中甲箱中有四个球,乙箱中有三个球(每个球的大小、形状完全相同),每一个箱子中只有一个红球,其余都是黑球. 若摸中甲箱中的红球,则可获奖金 元,若摸中乙箱中的红球,则可获奖金
元,若摸中乙箱中的红球,则可获奖金 元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
元. 活动规定:①参与者每个箱子只能摸一次,一次摸一个球;②可选择先摸甲箱,也可先摸乙箱;③如果在第一个箱子中摸到红球,则可继续在第二个箱子中摸球,否则活动终止.
(1)如果参与者先在乙箱中摸球,求其恰好获得奖金 元的概率;
元的概率;
(2)若要使得该参与者获奖金额的期望值较大,请你帮他设计摸箱子的顺序,并说明理由.
(本小题满分14分)已知向量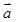 =(
=( ,1),向量
,1),向量 =(sin2x,cos2x),函数
=(sin2x,cos2x),函数
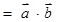
(1)求函数 的表达式,并作出函数
的表达式,并作出函数 在一个周期内的简图(用五点法列表描点);
在一个周期内的简图(用五点法列表描点);
(2)求函数 的周期,并写单调区间.
的周期,并写单调区间.
已知函数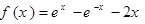 ,
,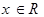
(1)证明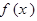 为奇函数,并在
为奇函数,并在 上为增函数;
上为增函数;
(2)若关于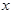 的不等式
的不等式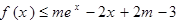 在
在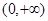 上恒成立,求实数
上恒成立,求实数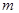 的取值范围
的取值范围
(3)设 ,当
,当 时,
时,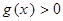 ,求
,求 的最大值
的最大值
设数列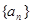 的前
的前 项和为
项和为
(1)若数列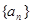 是首项为1,公比为2的等比数列,求常数
是首项为1,公比为2的等比数列,求常数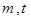 的值,使
的值,使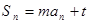 对一切大于零的自然数
对一切大于零的自然数 都成立
都成立
(2)若数列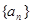 是首项为
是首项为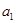 ,公差
,公差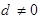 的等差数列,证明:存在常数
的等差数列,证明:存在常数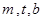 使得
使得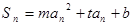 对一切大于零的自然数
对一切大于零的自然数 都成立,且
都成立,且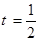
(3)若数列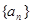 满足
满足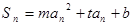 ,
,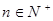 ,
,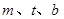 (
(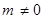 )为常数,且
)为常数,且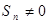 ,证明:当
,证明:当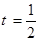 时,数列
时,数列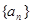 为等差数列
为等差数列
为迎接省运会在我市召开,美化城市,在某主干道上布置系列大型花盆,该圆形花盆直径2米,内部划分为不同区域种植不同花草 如图所示,在蝶形区域内种植百日红,该蝶形区域由四个对称的全等三角形组成,其中一个三角形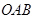 的顶点
的顶点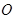 为圆心,
为圆心, 在圆周上,
在圆周上,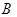 在半径
在半径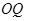 上,设计要求
上,设计要求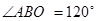

(1)请设置一个变量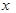 ,写出该蝶形区域的面积
,写出该蝶形区域的面积 关于
关于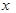 的函数表达式;
的函数表达式;
(2)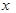 为多少时,该蝶形区域面积
为多少时,该蝶形区域面积 最大?
最大?
设椭圆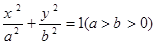 的左焦点为
的左焦点为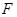 ,短轴上端点为
,短轴上端点为 ,连接
,连接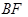 并延长交椭圆于点
并延长交椭圆于点 ,连接
,连接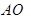 并延长交椭圆于点
并延长交椭圆于点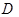 ,过
,过 三点的圆的圆心为
三点的圆的圆心为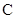
(1)若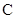 的坐标为
的坐标为 ,求椭圆方程和圆
,求椭圆方程和圆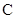 的方程;
的方程;
(2)若 为圆
为圆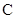 的切线,求椭圆的离心率
的切线,求椭圆的离心率