(本题8分)已知直线 被抛物线C:
被抛物线C: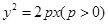 截得的弦长
截得的弦长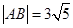 .
.
(1)求抛物线C的方程;
(2)若抛物线C的焦点为F,求三角形ABF的面积.
(本小题满分12分)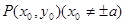 是双曲线
是双曲线 上一点,
上一点,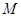 、
、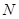 分别是双曲线
分别是双曲线 的左、右顶点,直线
的左、右顶点,直线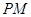 、
、 的斜率之积为
的斜率之积为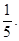
(I)求双曲线的离心率;
(II)过双曲线 的右焦点且斜率为1的直线交双曲线
的右焦点且斜率为1的直线交双曲线 于
于 两点,
两点,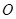 为坐标原点,
为坐标原点, 为双曲线上一点,满足
为双曲线上一点,满足 ,求
,求 的值.
的值.
.(本小题满分12分)已知数列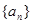 的前n项和为
的前n项和为 ,若
,若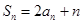 ,且
,且 ,数列
,数列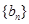 的前n项和为
的前n项和为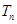 .
.
(I)求证: 为等比数列;
为等比数列;
(Ⅱ)求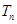 ;
;
(III)设 ,求证:
,求证:
.(本小题满分12分)设函数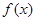 定义在
定义在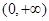 上,
上,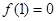 ,导函数
,导函数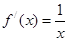 ,
,
(I)讨论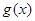 与
与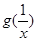 的大小关系;
的大小关系;
(II)求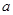 的取值范围,使得
的取值范围,使得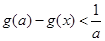 对任意
对任意 成立.
成立.
(本小题满分12分)红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立.
(I)求红队至少两名队员获胜的概率;
(II)用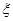 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求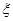 的分布列和数学期望
的分布列和数学期望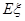 .
.