设函数f(x)=x3+ax2+bx在点x=1处有极值-2.
(1)求常数a,b的值;
(2)求曲线y=f(x)与x轴所围成的图形的面积.
已知椭圆P的中心O在坐标原点,焦点在 轴上,且经过点A(0,
轴上,且经过点A(0, ),离心率为
),离心率为 。
。
(1)求椭圆P的方程;
(2)是否存在过点E(0,-4)的直线 交椭圆P于两不同点
交椭圆P于两不同点 ,
, ,且满足
,且满足 ,若存在,求直线
,若存在,求直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
 的图象在
的图象在 处的切线方程为
处的切线方程为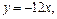
(1)求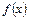 的解析式;
的解析式;
(2)求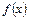 在
在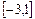 上的最值。
上的最值。
求过圆 的圆心且与极轴垂直的直线的极坐标方程。
的圆心且与极轴垂直的直线的极坐标方程。
定义在定义域D内的函数 ,若对任意的
,若对任意的
都有 则称函数
则称函数 为“Storm函数”。
为“Storm函数”。
已知函数
( 1 )若 求过点
求过点 处的切线方程;
处的切线方程;
( 2 )函数 是否为“Storm函数”?若是,给出证明;
是否为“Storm函数”?若是,给出证明;
若不是,说明理由。
甲乙两运动员进行射击训练,已知他们击中目标的环数都稳定在7,8,9,10环,且每次射击成绩互不影响,射击环数的频率分布表如下,
甲运动员乙运动员
| 射击环数 |
频数 |
频率 |
| 7 |
8 |
0.1 |
| 8 |
12 |
0.15 |
| 9 |
Z |
|
| 10 |
0.35 |
|
| 合计 |
80 |
1 |
| 射击环数 |
频数 |
频率 |
| 7 |
10 |
0.1 |
| 8 |
10 |
0.1 |
| 9 |
X |
0.45 |
| 10 |
35 |
Y |
| 合计 |
100 |
1 |
若将频率视为概率,回答下列问题,
(1)求甲运动员击中10环的概率;
(2)求甲运动员在3次射击中至少有一次击中9环以上(含9环)的概率;
(3)若甲运动员射击2次,乙运动员射击1次, 表示这3次射击中击中9环以上(含9环)的次数,求
表示这3次射击中击中9环以上(含9环)的次数,求 的分布列以及
的分布列以及 。
。