甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x),g(x)以及任意的x≥0,当甲公司投入x万元做宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元做宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司这一新产品的开发有失败的风险,否则没有失败的风险.
(1)试解释f(0)=10,g(0)=20的实际意义;
(2)设f(x)=  x+10,g(x)=
x+10,g(x)= +20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
+20,甲、乙两公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
函数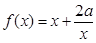 。
。
(1) 判断并证明函数的奇偶性;
(2) 若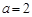 ,证明函数在(2,+
,证明函数在(2,+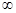 )单调增;
)单调增;
(3) 对任意的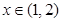 ,
, 恒成立,求
恒成立,求 的范围。
的范围。
函数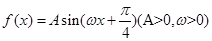 的最大值2,其图象相邻两条对称轴之间的距离为
的最大值2,其图象相邻两条对称轴之间的距离为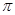 。
。
(1)求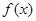 的解析式;
的解析式;
(2)求函数的单调增区间;
(1)求值: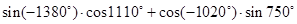 ;
;
(2)已知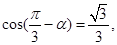 求
求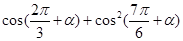 的值。
的值。
已知数列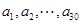 ,其中
,其中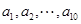 是首项为1,公差为1的等差数列;
是首项为1,公差为1的等差数列;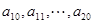 是公差为
是公差为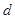 的等差数列;
的等差数列;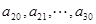 是公差为
是公差为 的等差数列(
的等差数列(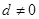 ).
).
(Ⅰ)若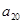 = 30,求
= 30,求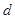 ;
;
(Ⅱ)试写出a30关于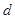 的关系式,并求a30的取值范围;
的关系式,并求a30的取值范围;
(Ⅲ)续写已知数列,可以使得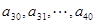 是公差为
是公差为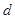 3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出
3的等差数列,请你依次类推,把已知数列推广为无穷数列,试写出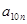 关于
关于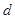 的关系式(
的关系式(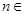 N
N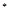 );
);
(Ⅳ)在(Ⅲ)条件下,且 ,试用
,试用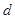 表示此数列的前100项和
表示此数列的前100项和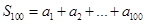
经过长期的观测得到:在交通繁忙时段,某公路段汽车的车流量y(千辆/小时)与汽车的平均速度v(千米/小时)之间的函数关系为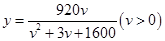 .
.
(1)在该时段内,当汽车的平均速度v为多少时,车流量最大?最大车流量为多少?
(精确到0.1千辆/小时)
(2)若要求在该时段内车流量超过10千辆/小时,则汽车的平均速度应在什么范围内?