已知{an}是各项都为正数的等比数列,数列{bn}满足bn= [lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
[lga1+lga2+lga3+…+lg(kan)],问是否存在正数k,使得{bn}成等差数列?若存在,求出k的值;若不存在,请说明理由.
(本小题满分12分)
已知向量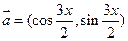 ,
,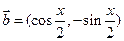 ,且
,且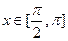 .
.
(1)求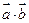 及
及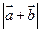 ;
;
(2)求函数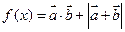 的最大值,并求使函数取得最大值时
的最大值,并求使函数取得最大值时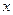 的
的
(本小题满分12分)解下列不等式:
(1)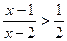 (2)、
(2)、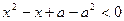
(本小题满分15分)
已知函数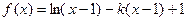 。
。
(I)求函数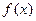 的单调区间;
的单调区间;
(II)若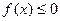 恒成立,试确定实数k的取值范围;
恒成立,试确定实数k的取值范围;
(III)证明: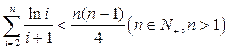 .
.
本小题满分15分)
已知 ,
, ,
, 的图像与
的图像与 轴交于点
轴交于点 ,且在该点处切线的斜率为
,且在该点处切线的斜率为 .
.
(I)若点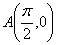 ,点
,点 是函数
是函数 图像上一点,
图像上一点, 是
是 的中点,当
的中点,当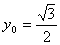 ,
,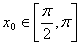 时,求
时,求 的值;
的值;
(II)当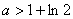 时,试问:是否存在曲线
时,试问:是否存在曲线 与
与 的公切线?并证明你的结论.
的公切线?并证明你的结论.
(本小题满分14分)
某企业投入81万元经销某产品,经销时间共60个月,市场调研表明,该企业在经销这个产品期间第 个月的利润
个月的利润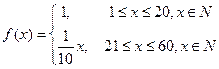 (单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第
(单位:万元),为了获得更多的利润,企业将每月获得的利润投入到次月的经营中,记第 个月的当月利润率
个月的当月利润率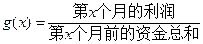 ,例如:
,例如: .
.
(I)求第 个月的当月利润率
个月的当月利润率 的表达式;
的表达式;
(II)该企业经销此产品期间,哪一个月的当月利润率最大,并求该月的当月利润率.