已知函数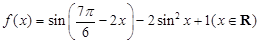 ,
,
(Ⅰ)求函数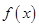 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(Ⅱ)在 中,三内角
中,三内角 ,
,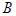 ,
,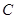 的对边分别为
的对边分别为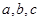 ,已知函数
,已知函数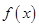 的图象经过点
的图象经过点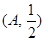 ,
,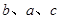 成等差数列,且
成等差数列,且 ,求
,求 的值.
的值.
如图,函数y=2sin(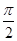 x+φ) x∈R , 其中0≤φ≤
x+φ) x∈R , 其中0≤φ≤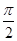 的图象与y轴交于点(0,1).
的图象与y轴交于点(0,1).
(Ⅰ)求φ的值;
(Ⅱ)设P是图象上的最高点,M、N是图象与x轴的交点,求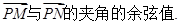
已知a,b,c分别为△ABC内角A,B,C的对边,sin2B=2sinAsinC
(Ⅰ)若a=b,求cosB;
(Ⅱ)设B=90°,且a= ,求△ABC的面积.
,求△ABC的面积.
在等比数列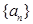 中,
中,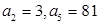 .
.
(Ⅰ)求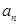 及其前
及其前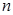 项和
项和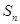 ;
;
(Ⅱ)设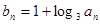 ,求数列
,求数列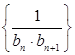 的前
的前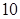 项和
项和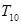 .
.
已知数列 满足
满足 (
( 为常数,
为常数, ).
).
(Ⅰ)当 时,求
时,求 ;
;
(Ⅱ)当 时,求
时,求 的值;
的值;
(Ⅲ)问:使 恒成立的常数
恒成立的常数 是否存在?并证明你的结论.
是否存在?并证明你的结论.