某摩托车生产企业,上年度生产摩托车的投入成本为1万元/辆,出厂价为1.2万元/辆,年销售量为1 000辆.本年度为适应市场需求,计划提高产品档次,适度增加投入成本.若每辆车投入成本增加的比例为x (0<x<1),则出厂价相应提高的比例为0.75x, 同时预计年销售量增加的比例为0.6x.已知年利润=(出厂价-投入成本)×年销售量.
(1)写出本年度预计的年利润y与投入成本增加的比例x的关系式;
(2)为使本年度利润比上年有所增加,问投入成本增加的比例x应在什么范围内?
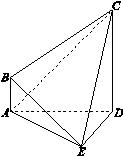
(本小题满分12分)如图,在四棱锥 中,
中, ,
, 平面
平面 ,
,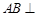 平面
平面 ,
,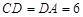 ,
,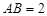 ,
,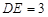 .
.
(Ⅰ)求棱锥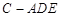 的体积;
的体积;
(Ⅱ)求证:平面
 平面
平面 ;
;
(Ⅲ)在线段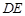 上是否存在一点
上是否存在一点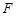 ,使
,使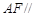 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(本小题满分12分)在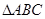 中,内角
中,内角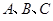 的对边分别为
的对边分别为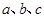 ,
,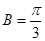 .
.
(Ⅰ)若 ,
, ,求
,求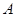 和
和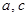 ;
;
(Ⅱ) 若 ,且
,且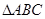 的面积为2
的面积为2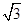 ,求
,求 的大小.
的大小.
(本小题满分12分)某中学刚搬迁到新校区,学校考虑,若非住校生上学路上单程所需时间人均超过20分钟,则学校推迟5分钟上课.为此,校方随机抽取100个非住校生,调查其上学路上单程所需时间(单位:分钟),根据所得数据绘制成如下频率分布直方图,其中时间分组为 ,
, ,
, ,
, ,
, .
.
(Ⅰ)求频率分布直方图中 的值;
的值;
(Ⅱ)从统计学的角度说明学校是否需要推迟5分钟上课;
(Ⅲ)若从样本单程时间不小于30分钟的学生中,随机抽取2人,求恰有一个学生的单程时间落在 上的概率.
上的概率.
(本小题满分12分)设数列 的前
的前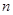 项和为
项和为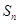 ,且
,且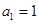 ,
,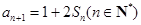 .
.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列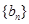 为等差数列,且
为等差数列,且 ,公差为
,公差为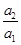 .当
.当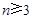 时,比较
时,比较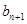 与
与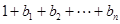 的大小.
的大小.
(本小题满分14分)已知函数 .
.
(1)当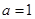 时,求函数
时,求函数 图象在点
图象在点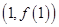 处的切线方程;
处的切线方程;
(2)当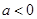 时,讨论函数
时,讨论函数 的单调性;
的单调性;