(本小题满分12分)如图,在四棱锥 中,
中, ,
, 平面
平面 ,
, 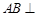 平面
平面 ,
,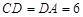 ,
,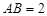 ,
,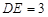 .
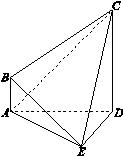
.
(Ⅰ)求棱锥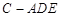 的体积;
的体积;
(Ⅱ)求证:平面
 平面
平面 ;
;
(Ⅲ)在线段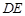 上是否存在一点
上是否存在一点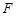 ,使
,使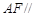 平面
平面 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
化简: (其中
(其中 为第三象限角).
为第三象限角).
已知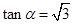 ,
, ,求
,求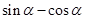 的值.
的值.
设函数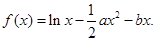
(Ⅰ)当 时,求
时,求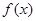 的最大值;
的最大值;
(Ⅱ)令 ,(
,( ),其图象上任意一点
),其图象上任意一点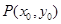 处切线的斜率
处切线的斜率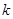 ≤
≤ 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅲ)当 ,
, ,方程
,方程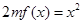 有唯一实数解,求正数
有唯一实数解,求正数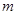 的值.
的值.
已知椭圆 的离心率为
的离心率为 ,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
,直线l:y=x+2与以原点为圆心、椭圆C1的短半轴长为半径的圆O相切。
(Ⅰ)求椭圆C1的方程;
(Ⅱ)设椭圆C1的左焦点为F1,右焦点为F2,直线l1过点F1,且垂直于椭圆的长轴,动直线l2垂直于l1,垂足为点P,线段PF2的垂直平分线交l2于点M,求点M的轨迹C2的方程;
(Ⅲ)设C2与x轴交于点Q,不同的两点R、S在C2上,且 满足 ,求
,求 的取值范围。
的取值范围。
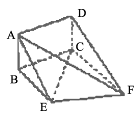
如图,矩形ABCD和梯形BEFC所在平面互相垂直,BE//CF, BCF=
BCF= CEF=
CEF=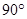 ,AD=
,AD=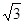 ,EF=2.
,EF=2.
(Ⅰ)求证:AE//平面DCF;
(Ⅱ)当AB的长为何值时,二面角A-EF-C的大小为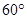 .
.