某租赁公司拥有汽车100辆.当每辆车的月租金为3 000元时,可全部租出.当每辆车的月租金每增加50元时,未租出的车将会增加一辆.租出的车每月需要维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3 600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
已知数列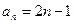 ,数列
,数列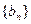 的前n项和为
的前n项和为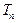 ,满足
,满足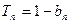
(1)求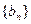 的通项公式;
的通项公式;
(2)试写出一个m,使得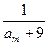 是
是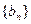 中的项.
中的项.
从装有编号分别为a,b的2个黄球和编号分别为 c,d的2个红球的袋中无放回地摸球,每次任摸一球,求:
(1)第1次摸到黄球的概率;(2)第2次摸到黄球的概率.
已知数列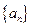 是首项
是首项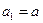 ,公差为2的等差数列,数列
,公差为2的等差数列,数列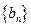 满足
满足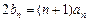 ;
;
(1)若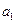 、
、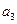 、
、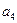 成等比数列,求数列
成等比数列,求数列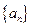 的通项公式;
的通项公式;
(2)若对任意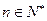 都有
都有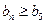 成立,求实数
成立,求实数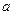 的取值范围;
的取值范围;
(3)数列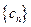 满足
满足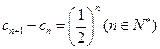 ,其中
,其中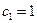 ,
,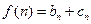 ,当
,当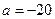 时,求
时,求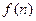 的最小值(
的最小值(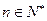 ).
).
已知抛物线C的顶点在原点,焦点为F(0,1),且过点A(2,t),
(1)求t的值;
(2)若点P、Q是抛物线C上两动点,且直线AP与AQ的斜率互为相反数,试问直线PQ的斜率是否为定值,若是,求出这个值;若不是,请说明理由.
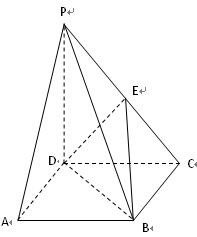
四棱锥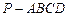 的底面
的底面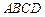 是正方形,侧棱
是正方形,侧棱 ⊥底面
⊥底面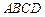 ,
,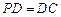 ,
,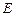 是
是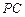 的中点.
的中点.
(1)证明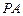 //平面
//平面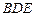 ;
;
(2)求二面角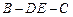 的平面角的余弦值;
的平面角的余弦值;
(3)在棱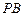 上是否存在点
上是否存在点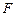 ,使
,使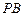 ⊥平面
⊥平面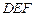 ?
?
若存在,请求出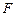 点的位置;若不存在,请说明理由.
点的位置;若不存在,请说明理由.