已知椭圆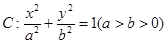 的左右焦点分别是
的左右焦点分别是 ,离心率
,离心率 ,
,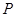 为椭圆上任一点,且
为椭圆上任一点,且 的最大面积为
的最大面积为 .
.
(Ⅰ)求椭圆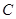 的方程;
的方程;
(Ⅱ)设斜率为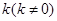 的直线
的直线 交椭圆
交椭圆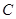 于
于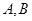 两点,且以
两点,且以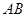 为直径的圆恒过原点
为直径的圆恒过原点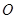 ,若实数
,若实数 满足条件
满足条件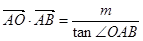 ,求
,求 的最大值.
的最大值.
已知函数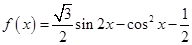 .
.
(1)求函数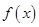 的最小值和最小正周期;
的最小值和最小正周期;
(2)设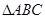 的内角
的内角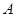 ,
,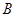 ,
,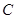 的对边分别为
的对边分别为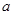 ,
,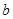 ,
,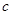 ,且
,且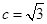 ,
,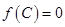 ,若
,若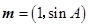 与
与 共线,求
共线,求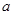 ,
,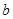 的值.
的值.
已知 ;
; ,若
,若 是
是 的充分而不必要条件,求实数
的充分而不必要条件,求实数 的范围.
的范围.
(本小题满分12分)
已知函数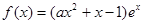 ,其中
,其中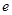 是自然对数的底数,
是自然对数的底数,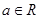 .
.
(1)若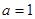 ,求曲线
,求曲线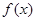 在点
在点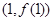 处的切线方程;
处的切线方程;
(2)若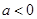 ,求
,求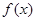 的单调区间;
的单调区间;
(3)若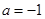 ,函数
,函数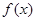 的图象与函数
的图象与函数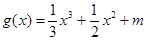 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数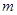 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆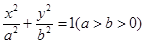 的左右焦点分别为
的左右焦点分别为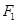 、
、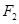 ,由4个点
,由4个点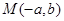 、
、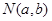 、
、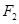 和
和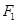 组成一个高为
组成一个高为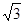 ,面积为
,面积为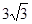 的等腰梯形.
的等腰梯形.
(1)求椭圆的方程;
(2)过点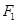 的直线和椭圆交于
的直线和椭圆交于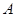 、
、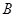 两点,求
两点,求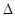
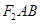 面积的最大值.
面积的最大值.
(本小题满分12分)
如图,三棱柱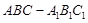 中,
中,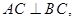
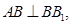
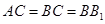 ,
,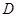 为
为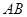 的中点,且
的中点,且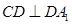 .
.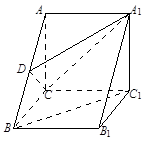
(1)求证: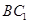 ∥平面
∥平面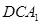 ;
;
(2)求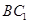 与平面
与平面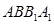 所成角的大小.
所成角的大小.