已知函数y=f(x)对任意x,y∈R均有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)="-"  .
.
(1)判断并证明f(x)在R上的单调性;
(2)求f(x)在[-3,3]上的最值.
设对于不大于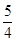 的所有正实数
的所有正实数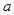 ,如果满足不等式
,如果满足不等式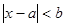 的一切实数
的一切实数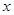 ,也满足不等式
,也满足不等式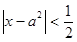 ,求实数
,求实数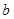 的取值范围。
的取值范围。
已知以角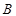 为钝角的
为钝角的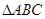 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c, ,
,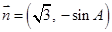 ,且
,且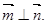
(1)求角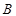 的大小;
的大小;
(2)求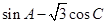 的取值范围.
的取值范围.
已知集合A=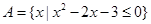 ,
,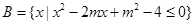
(1)若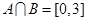 ,求实数
,求实数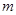 的值;
的值;
(2)若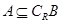 ,求实数
,求实数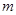 的取值范围.
的取值范围.
(本小题满分14分)设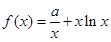 ,
,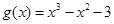 .
.
(1)当 时,求曲线
时,求曲线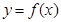 在
在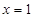 处的切线方程;
处的切线方程;
(2)如果存在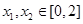 ,使得
,使得 成立,求满足上述条件的最大整数
成立,求满足上述条件的最大整数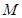 ;
;
(3)如果对任意的 ,都有
,都有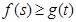 成立,求实数
成立,求实数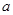 的取值范围.
的取值范围.
(本小题满分13分)已知几何体A—BCED的三视图如图所示,其中俯视图和侧视图都是腰长为4的等腰直角三角形,正视图为直角梯形.
(1)求此几何体的体积V的大小;
(2)求异面直线DE与AB所成角的余弦值;
(3)试探究在DE上是否存在点Q,使得AQ BQ并说明理由.
BQ并说明理由.