假设某市2008年新建住房400万平方米,其中有250万平方米是中低价房,预计在今后的若干年内,该市每年新建住房面积平均比上一年增长8%.另外,每年新建住房中,中低价房的面积均比上一年增加50万平方米.那么,到哪一年底,
(1)该市历年所建中低价房的累计面积(以2008年为累计的第一年)将首次不少于4 750万平方米?
(2)当年建造的中低价房的面积占该年建造住房面积的比例首次大于85%?(参考数据:1.084≈1.36,1.085≈1.47,
1.086≈1.59)
已知曲线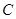 的极坐标方程是
的极坐标方程是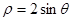 ,直线
,直线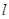 的参数方程是
的参数方程是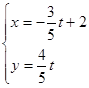 (
(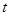 为参数).
为参数).
(I)将曲线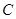 的极坐标方程转化为直角坐标方程;
的极坐标方程转化为直角坐标方程;
(Ⅱ)设直线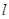 与
与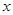 轴的交点是
轴的交点是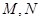 为曲线
为曲线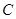 上一动点,求
上一动点,求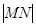 的最大值.
的最大值.
曲线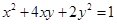 在二阶矩阵
在二阶矩阵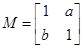 的作用下变换为曲线
的作用下变换为曲线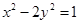 ,
,
(I)求实数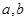 的值;
的值;
(II)求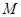 的逆矩阵
的逆矩阵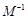 .
.
已知函数 .
.
(I)若 在
在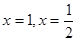 处取得极值,
处取得极值,
①求 、
、 的值;②存在
的值;②存在 ,使得不等式
,使得不等式 成立,求
成立,求 的最小值;
的最小值;
(II)当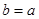 时,若
时,若 在
在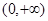 上是单调函数,求
上是单调函数,求 的取值范围.(参考数据
的取值范围.(参考数据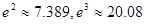 )
)
如图,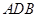 为半圆,
为半圆,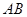 为半圆直径,
为半圆直径,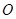 为半圆圆心,且
为半圆圆心,且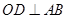 ,
, 为线段
为线段 的中点,已知
的中点,已知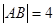 ,曲线
,曲线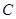 过
过 点,动点
点,动点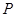 在曲线
在曲线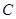 上运动且保持
上运动且保持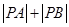 的值不变.
的值不变.
(I)建立适当的平面直角坐标系,求曲线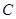 的方程;
的方程;
(II)过点 的直线
的直线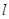 与曲线
与曲线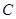 交于
交于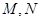 两点,与
两点,与 所在直线交于
所在直线交于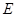 点,
点, ,
,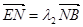 证明:
证明: 为定值.
为定值.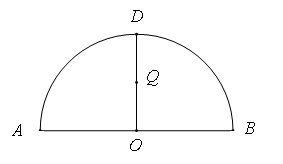
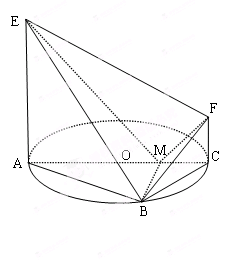
如图,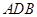 是圆
是圆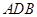 的直径,点
的直径,点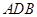 在圆
在圆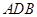 上,
上,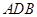 ,
,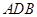 交
交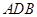 于点
于点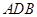 ,
,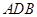 平面
平面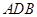 ,
,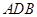 ,
,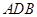 .
.
(1)证明: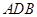 ;
;
(2)求平面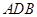 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.