已知函数f(x)=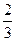 x3-2ax2+3x(x∈R).
x3-2ax2+3x(x∈R).
(1)若a=1,点P为曲线y=f(x)上的一个动点,求以点P为切点的切线斜率取最小值时的切线方程;
(2)若函数y=f(x)在(0,+∞)上为单调增函数,试求满足条件的最大整数a.
设 是定义在(0,+∞)上的单调增函数,满足
是定义在(0,+∞)上的单调增函数,满足 ,
, 求:(1)f(1) ,f(9);(2)若
求:(1)f(1) ,f(9);(2)若 ,求x的取值范围。
,求x的取值范围。
已知 是定义在
是定义在 上的奇函数,当
上的奇函数,当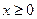 时,
时,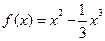 , (1)求函数
, (1)求函数 的解析式;(2)讨论函数
的解析式;(2)讨论函数 的单调性.
的单调性.
已知p:方程x2+mx+1=0有两个不等的负实根,q:方程4x2+4(m-2)x+1=0无实根,若p或q为真,p且q为假。求实数m的取值范围。
已知集合A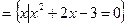 ,B=
,B=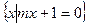 ,且
,且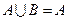 ,求实数
,求实数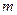 的取值范围.
的取值范围.
(本小题满分14分)一个口袋中装有 个红球
个红球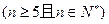 和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
和5个白球,一次摸奖从中摸两球,两个球颜色不同则为中奖。
(1)试用 表示一次摸奖中奖的概率
表示一次摸奖中奖的概率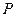 ;
;
(2)若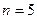 ,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
,求三次摸奖(每次摸奖后放回)恰有一次中奖的概率;
(3)记三次摸奖(每次摸奖后放回)恰有一次中奖的概率为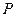 ,当
,当 取多少时,
取多少时,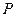 最大?
最大?