将编号为1,2,…,9的九个小球随机放置在圆周的九个等分点上,每个等分点上各有一个小球.设圆周上所有相邻两球号码之差的绝对值之和为要S.求使S达到最小值的放法的概率.(注:如果某种放法,经旋转或镜面反射后可与另一种放法重合,则认为是相同的放法)
已知数列{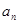 }是等差数列,其中每一项及公差
}是等差数列,其中每一项及公差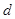 均不为零,设
均不为零,设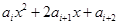 =0(
=0( )是关于
)是关于 的一组方程.
的一组方程.
(1)求所有这些方程的公共根;
(2)设这些方程的另一个根为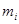 ,求证
,求证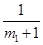 ,
,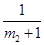 ,
, ,…,
,…, 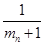 ,…也成等差数列.
,…也成等差数列.
老峰镇计划建造一个室内面积为800 的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室。在温室内,沿左.右两侧与后侧内墙各保留1 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3  宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
宽的空地。当矩形温室的边长各为多少时?蔬菜的种植面积最大。最大种植面积是多少?
在 中,
中, ,
, .
.
(1)求角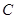 的大小;
的大小;
(2)若 最大边的边长为
最大边的边长为 ,求最小边的边长.
,求最小边的边长.
在ABC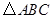 中,已知B=45AD=5,Ac=7,Dc=3
中,已知B=45AD=5,Ac=7,Dc=3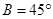 ,
,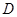 是
是 上一点,
上一点,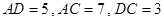 ,求
,求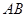 的长.
的长.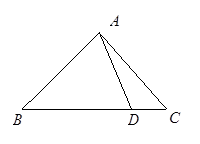
已知等比数列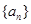 中,
中,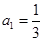 ,公比
,公比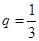 ,
,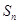 为
为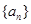 的前n项和.
的前n项和.
(1)求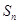
(2)设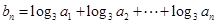 ,求数列
,求数列 的通项公式.
的通项公式.