如图所示，一质量为m=30kg的弹性小球A（可视作质点），在左侧平台上滑行一段距离后平抛，恰能无碰撞地沿圆弧切线从M点进入光滑竖直圆弧轨道，并沿轨道下滑，M、N为圆弧两端点，其连线水平．已知圆弧半径为R=1.0m，对应圆心角为θ=1060，平台与MN连线的高度差为h=0.8m．（计算中取g=10m/s2，sin530=0.8，cos530=0.6）求：
(1) 球A平抛的初速度；
(2) 球A运动到圆弧轨道最低点时，恰好与停在那里的与A完全相同的小球B发生弹性碰撞，求碰撞发生后A、B小球对轨道最低点的压力各为多大。
游乐场的过山车的运动过程可以抽象为图所示模型。弧形轨道下端与圆轨道相接，使小球从弧形轨道上端A点静止滑下，进入圆轨道后沿圆轨道运动，最后离开。试分析A点离地面的高度h至少要多大，小球才可以顺利通过圆轨道最高点（已知圆轨道的半径为R，不考虑摩擦等阻力）。
长为L的细线，拴一质量为m的小球，一端固定于O点，让其在水平面内做匀速圆周运动（这种运动通常称为圆锥摆运动），如图所示，当摆线L与竖直方向的夹角是α时，求：
（1）线的拉力F；
（2）小球运动的线速度的大小；
（3）小球运动的角速度及周期。
如图所示，有一个很深的竖直井，井的横截面为一个圆，半径为
，且井壁光滑，有一个小球从井口的一侧以水平速度
抛出与井壁发生碰撞，撞后以原速率被反弹，求小球与井壁发生第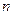
次碰撞处的深度。
如图所示，半径为R的圆板做匀速运动，当半径OB转到某一方向时，在圆板中心正上方h处以平行于OB方向水平抛出一球，小球抛出时的速度及圆盘转动的角速度为多少时，小球与圆盘只碰撞一次，且落点为B。
如图所示，某圆筒绕中心轴线沿顺时针方向做匀速圆周运动，筒壁上有两个位于同一圆平面内的小孔A、B，A、B与轴的垂直连线之间的夹角为θ，一质点（质量不计）在某时刻沿A孔所在直径方向匀速射入圆筒，恰从B孔穿出，若质点匀速运动的速度为v，圆筒半径为R．则，圆筒转动的角速度为____________。