抽气机每次抽出容器内空气的60%,要使容器内的空气少于原来的0.1%,则至少要抽几次.(lg2≈0.301 0)
已知函数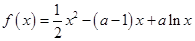 ,其中常数
,其中常数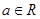 .
.
(Ⅰ)当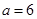 时,求函数
时,求函数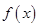 的极值点;
的极值点;
(Ⅱ)证明:对任意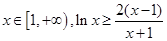 恒成立;
恒成立;
(Ⅲ)对于函数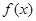 图象上的不同两点
图象上的不同两点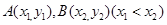 ,如果在函数
,如果在函数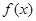 图象上存在点
图象上存在点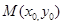 (其中
(其中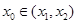 ),使得在点M处的切线
),使得在点M处的切线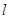 ∥AB,则称直线AB存在“伴侣切线”.特别地,当
∥AB,则称直线AB存在“伴侣切线”.特别地,当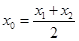 ,又称直线AB存在“中值伴侣切线”.
,又称直线AB存在“中值伴侣切线”.
试问:当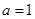 时,对于函数
时,对于函数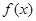 图象上不同两点A、B,直线AB是否存在“中值伴侣切线”,并证明你的结论.
图象上不同两点A、B,直线AB是否存在“中值伴侣切线”,并证明你的结论.
已知椭圆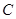 :
: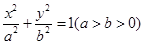 ,
,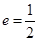 ,其中
,其中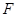 是椭圆的右焦点,焦距为
是椭圆的右焦点,焦距为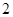 ,直线
,直线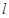 与椭圆
与椭圆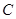 交于点
交于点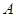 ,
,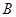 ,点
,点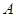 ,
,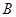 的中点横坐标为
的中点横坐标为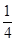 ,且
,且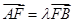 (其中
(其中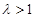 ).
).
(1)求椭圆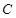 的标准方程;
的标准方程;
(2)求实数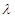 的值.
的值.
已知三棱柱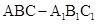 中,侧棱垂直于底面,
中,侧棱垂直于底面,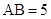 ,
,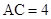 ,
,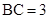 ,
,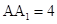 ,点
,点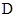 在
在 上.
上.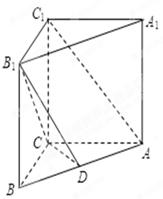
(1)若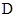 是
是 中点,求证:
中点,求证: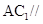 平面
平面 ;
;
(2)当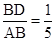 时,求二面角
时,求二面角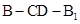 的余弦值.
的余弦值.
一位网民在网上光顾某淘宝小店,经过一番浏览后,对该店铺中的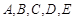 五种商品有购买意向.已知该网民购买
五种商品有购买意向.已知该网民购买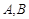 两种商品的概率均为
两种商品的概率均为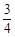 ,购买
,购买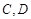 两种商品的概率均为
两种商品的概率均为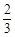 ,购买
,购买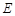 种商品的概率为
种商品的概率为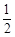 .假设该网民是否购买这五种商品相互独立.
.假设该网民是否购买这五种商品相互独立.
(1)求该网民至少购买4种商品的概率;
(2)用随机变量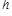 表示该网民购买商品的种数,求
表示该网民购买商品的种数,求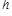 的概率分布和数学期望.
的概率分布和数学期望.
在△A BC,a,b,c分别是角A,B,C的对边,且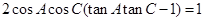 .
.
(Ⅰ)求B的大小;
(Ⅱ)若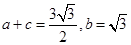 ,求△A BC的面积.
,求△A BC的面积.