如图,在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,SD=2a. 
(1)求证:平面SAB⊥平面SAD;
(2)设SB的中点为M,当 为何值时,能使DM⊥MC?请给出证明.
为何值时,能使DM⊥MC?请给出证明.
在 中,内角
中,内角 所对的边分别为
所对的边分别为 已知
已知 ,
,
(Ⅰ)求角 的取值范围;
的取值范围;
(Ⅱ)若 的面积
的面积 ,
, 为钝角,求角
为钝角,求角 的大小.
的大小.
已知函数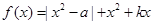 ,(
,(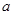 为常数且
为常数且 ).
).
(1)若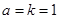 ,求不等式
,求不等式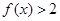 的解集;
的解集;
(2)若函数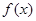 在
在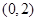 上有两个零点
上有两个零点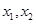 ,求
,求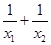 的取值范围.
的取值范围.
如图,已知抛物线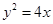 ,点
,点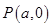 是x轴上的一点,经过点
是x轴上的一点,经过点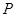 且斜率为1的直线
且斜率为1的直线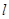 与抛物线相交于
与抛物线相交于 两点.
两点.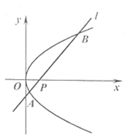
(1)求证线段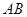 的中点在一条定直线上,并求出该直线方程;
的中点在一条定直线上,并求出该直线方程;
(2)若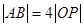 (O为坐标原点),求
(O为坐标原点),求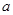 的值.
的值.
如图,在四棱锥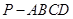 中,底面
中,底面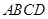 是菱形,
是菱形,
 ,
, ⊥平面
⊥平面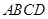 ,
, ,点
,点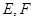 分别为
分别为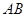 和
和 中点.
中点.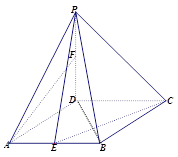
(1)求证:直线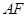
 平面
平面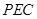 ;
;
(2)求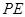 与平面
与平面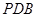 所成角的正弦值.
所成角的正弦值.
已知公差不为0的等差数列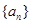 的前
的前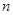 项和为
项和为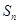 ,
,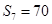 且
且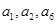 成等比数列。
成等比数列。
(1)求数列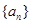 的通项公式;
的通项公式;
(2)设 ,数列
,数列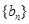 的最小项是第几项,并求出该项的值.
的最小项是第几项,并求出该项的值.