(本小题满分12分)已知A、B分别在射线CM、CN(不含端点C)上运动,∠MCN= π,在△ABC中,角A、B、C所对的边分别是a、b、c.
π,在△ABC中,角A、B、C所对的边分别是a、b、c.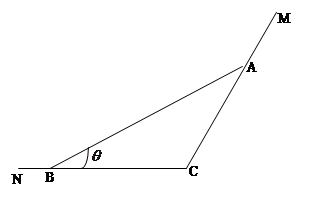
(Ⅰ)若a、b、c依次成等差数列,且公差为2.求c的值;
(Ⅱ)若c= ,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
,∠ABC=θ,试用θ表示△ABC的周长,并求周长的最大值.
(本小题满分10分)已知函数 .
.
(1)当 时,求
时,求 的解集;
的解集;
(2)当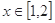 时,
时, 恒成立,求实数
恒成立,求实数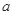 的集合.
的集合.
设函数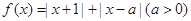
(1)若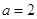 时,解不等式
时,解不等式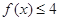 ;
;
(2)若不等式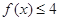 的对一切
的对一切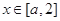 恒成立,求实数
恒成立,求实数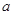 的取值范围.
的取值范围.
以原点为极点,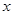 轴的非负半轴为极轴建立极坐标系.已知某圆的极坐标方程为
轴的非负半轴为极轴建立极坐标系.已知某圆的极坐标方程为
(1)将极坐标方程化为普通方程,并选择恰当的参数写出它的参数方程;
(2)若点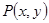 在该圆上,求
在该圆上,求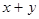 的最大值和最小值.
的最大值和最小值.
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点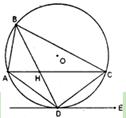
(1)求证:BD平分∠ABC
(2)若AB=4,AD=6,BD=8,求AH的长