已知空间四边形 中,
中, 分别是
分别是 上的点,且直线
上的点,且直线 与
与 交于点
交于点 ,求证
,求证 三点共线.
三点共线.
用0,1,2,3,4,5六个数字组成无重复数字的四位数,比3410大的四位数有多少个?
(本小题12分)定义运算: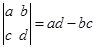
(1)若已知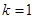 ,解关于
,解关于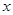 的不等式
的不等式
(2)若已知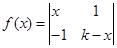 ,对任意
,对任意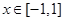 ,都有
,都有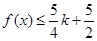 ,求实数
,求实数 的取值范围。
的取值范围。
(本小题12分)
已知函数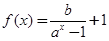
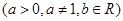 是奇函数,且
是奇函数,且
(1)求 ,
, 的值;
的值;
(2)用定义证明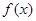 在区间
在区间 上是减函数.
上是减函数.
(本小题12分)若 ,函数
,函数 (其中
(其中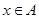 )
)
(1)求函数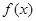 的定义域;
的定义域;
(2)求函数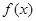 的值域
的值域
(本小题12分)
某市居民生活用水收费标准如下:
用水量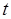 (吨) (吨) |
每吨收费标准(元) |
不超过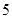 吨部分 吨部分 |
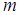 |
超过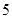 吨不超过 吨不超过 吨部分 吨部分 |
3 |
超过 吨部分 吨部分 |
 |
已知某用户一月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为 元;二月份用水量为
元;二月份用水量为 吨,缴纳的水费为
吨,缴纳的水费为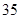 元.设某用户月用水量为
元.设某用户月用水量为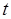 吨,交纳的水费为
吨,交纳的水费为 元.
元.
(1)写出 关于
关于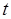 的函数关系式;
的函数关系式;
(2)若某用户希望三月份缴纳的水费不超过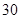 元,求该用户三月份最多可以用多少吨水?
元,求该用户三月份最多可以用多少吨水?