一个质量为5.0kg的石块从塔顶由静止下落,经过4.0s的时间落至地面。已知石块受到的空气阻力可忽略不计,重力加速度g=10m/s2。求:
(1)塔顶距离地面的高度。
(2)石块落地时重力对石块的功率。
某课外小组设计了一种测定风速的装置,其原理如图所示,一个劲度系数k=1300N/m,自然长度L0=0.5m弹簧一端固定在墙上的M点,另一端N与导电的迎风板相连,弹簧穿在光滑水平放置的电阻率较大的金属杆上,弹簧是不导电的材料制成的。迎风板面积S=0.5m2,工作时总是正对着风吹来的方向。电路的一端与迎风板相连,另一端在M点与金属杆相连。迎风板可在金属杆上滑动,且与金属杆接触良好。定值电阻R=1.0Ω,电源的电动势E=12V,内阻r=0.5Ω。闭合开关,没有风吹时,弹簧处于原长,电压表的示数U1=3.0V,某时刻由于风吹迎风板,电压表的示数变为U2=2.0V。(电压表可看作理想表)求:
(1)金属杆单位长度的电阻;
(2)此时作用在迎风板上的风力。
如图所示,在光滑水平地面上,有一质量m1= 4.0kg的平板小车,小车的右端有一固定的竖直挡板,挡板上固定一轻质细弹簧。位于小车上A点处质量m2=1.0kg的木块(可视为质点)与弹簧的左端相接触但不连接,此时弹簧与木块间无相互作用力。木块与A点左侧的车面之间的动摩擦因数μ= 0.40,木块与A点右侧的车面之间的摩擦可忽略不计。现小车与木块一起以v0= 2.0m/s的初速度向右运动,小车将与其右侧的竖直墙壁发生碰撞,已知碰撞时间极短,碰撞后小车以v 1= 1.0m/s的速度反向弹回,已知重力加速度g取10m/s2,弹簧始终处于弹性限度内。求:
(1)小车撞墙后弹簧的最大弹性势能;
(2)要使木块最终不从小车上滑落,则车面A点左侧粗糙部分的长度应满足什么条件?
如图所示,倾角θ=37°的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块,从距地面h=2.7m处沿斜面由静止开始下滑,小物块与斜面间的动摩擦因数μ=0.25,求:(sin37°=0.6,cos37°=0.8,g=10m/s2)
(1)物块滑到斜面底端B时的速度大小;
(2)物块运动到圆轨道的最高点A时,对圆轨道的压力大小。
一重为G的小球,套于竖直放置的半径为R的光滑大圆环上,一劲度系数为k,自然长度为L(L>2R)的轻质弹簧,其上端固定在大圆环的最高点,下端与小球相连,如图所示,不考虑一切摩擦,求小球静止时弹簧与竖直方向的夹角。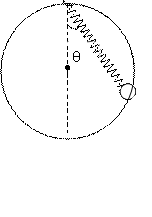
两极板M、N相距为d,板长为3d,两极板都未带电,板间有垂直于纸面向外的匀强磁场,如图11-3-18所示,一群电子沿平行于极板的方向从各个位置以速度V射入板间.为了使电子都不从板间穿出,磁感应强度B的取值范围是怎样的?(设电子电量为e、质量为m)