一场篮球比赛到了最后5分钟,甲队比乙队少得5分。如果甲队全投3分球,则有8次投篮机会。如果甲队全投2分球,则有3次投篮机会。假设甲队队员投3分球的命中率均为0.6,投2分球的命中率均为0 .8,并且甲队加强防守,不给乙队投篮机会.问全投3分球与全投2分球这两种方案中选择哪一种甲队获胜的概率较大?
某城市 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以 ,
, ,
, ,
, ,
, ,
, ,
, 分组的频率分布直方图如图.
分组的频率分布直方图如图.
(1)求直方图中 的值;
的值;
(2)求月平均用电量的众数和中位数;
(3)在月平均用电量为 ,
, ,
, ,
, 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取 户居民,则月平均用电量在
户居民,则月平均用电量在 的用户中应抽取多少户?
的用户中应抽取多少户?
已知△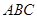 的内角
的内角 所对的边分别为
所对的边分别为 且
且 .
.
(1)若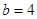 ,求
,求 的值;
的值;
(2)若△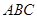 的面积
的面积 求
求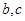 的值.
的值.
如图,在三棱柱 中,
中, ,
,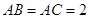 ,
,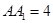 ,
,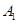 在底面ABC的射影为BC的中点,D为
在底面ABC的射影为BC的中点,D为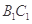 的中点.
的中点.
(1)证明: ;
;
(2)求直线 和平面
和平面 所成的角的正弦值.
所成的角的正弦值.
设数列 的前
的前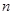 项和
项和 满足
满足 且
且 成等差数列.
成等差数列.
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设数列 的前
的前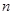 项和为
项和为 ,求
,求 .
.
在如图所示的多面体ABCDE中,AB∥DE,AB⊥AD,△ACD是正三角形,AD=DE=2AB=2,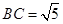 ,F是CD的中点.
,F是CD的中点.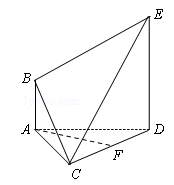
(Ⅰ)求证AF∥平面BCE;
(Ⅱ)求多面体ABCDE的体积.