已知函数f(x)=x|x2-a|（a∈R）,
(1)当a≤0时，求证函数f(x)在（-∞，+∞）上是增函数；
（2）当a=3时，求函数f(x)在区间［0，b］上的最大值
设函数f(x)=lnx-px+1
(1)当P>0时，若对任意x>0，恒有f(x)≤0,求P的取值范围
（2）证明：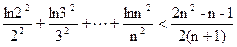
(n∈N
，n≥2)
设函数f(x)=sin(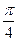
x-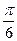
)-2cos2
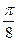x+1
（1）求f(x)的最小正周期
（2）若函数y=g(x)与f(x)的图象关于直线x=1对称，求当x∈[0,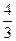
]时，y=g(x)的最大值
已知函数
，
（1）求
在x=1处的切线斜率的取值范围；
（2）求当在x=1处的切线的斜率最小时，的解析式；
（3）在（Ⅱ）的条件下，是否总存在实数m，使得对任意的
，总存在
，使得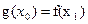
成立？若存在，求出实数m的取值范围；若不存在，说明理由．
数列
的前
项和为
，数列
的前项的和为
，为等差数列且各项均为正数，
，
，
（Ⅰ）求证：数列是等比数列；
（Ⅱ）若
，
，
成等比数列，求．
，当
时，
，求
的取值范围．