设 是直线上任意四点(顺序和位置都任意),且
是直线上任意四点(顺序和位置都任意),且 ,
,
求证: .
.
经销商经销某种农产品,在一个销售季度内,每售出1t该产品获利润500元,未售出的产品,每1t亏损300元。根据历史资料,得到销售季度内市场需求量的频率分布直方图,如右图所示。经销商为下一个销售季度购进了130t该农产品。以x(单位:t,100≤x≤150)表示下一个销售季度内经销该农产品的数量,T表示利润.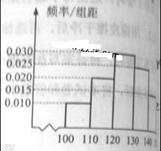
(1)将T表示为x的函数
(2)根据直方图估计利润T不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若x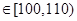 ,则取x=105,且x=105的概率等于需求量落入[100,110
,则取x=105,且x=105的概率等于需求量落入[100,110 ,求T的数学期望.
,求T的数学期望.
设袋子中装有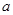 个红球,
个红球,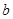 个黄球,
个黄球,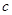 个蓝球,且规定:取出一个红球得1分,
个蓝球,且规定:取出一个红球得1分,
取出一个黄球2分,取出蓝球得3分。
(1)当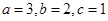 时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量
时,从该袋子中任取(有放回,且每球取到的机会均等)2个球,记随机变量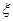 为取出此2球所得分数之和,.求
为取出此2球所得分数之和,.求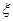 分布列;
分布列;
(2)从该袋子中任取(且每球取到的机会均等)1个球,记随机变量 为取出此球所得分数.若
为取出此球所得分数.若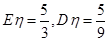 ,求
,求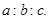
甲、乙两支排球队进行比赛,约定先胜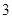 局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是
局者获得比赛的胜利,比赛随即结束。除第五局甲队获胜的概率是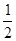 外,其余每局比赛甲队获胜的概率都是
外,其余每局比赛甲队获胜的概率都是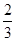 。假设各局比赛结果相互独立。
。假设各局比赛结果相互独立。
(1)分别求甲队以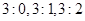 胜利的概率;
胜利的概率;
(2)若比赛结果为求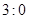 或
或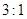 ,则胜利方得
,则胜利方得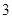 分,对方得
分,对方得 分;若比赛结果为
分;若比赛结果为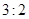 ,则胜利方得
,则胜利方得 分、对方得
分、对方得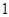 分。求乙队得分
分。求乙队得分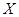 的分布列及数学期望。
的分布列及数学期望。
某联欢晚会举行抽奖活动,举办方设置了甲、乙两种抽奖方案,方案甲的中奖率为 ,中奖可以获得2分;方案乙的中奖率为
,中奖可以获得2分;方案乙的中奖率为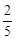 ,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
,中奖可以获得3分;未中奖则不得分。每人有且只有一次抽奖机会,每次抽奖中奖与否互不影响,晚会结束后凭分数兑换奖品。
(1)若小明选择方案甲抽奖,小红选择方案乙抽奖,记他们的累计得分为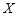 ,求
,求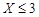 的概率;
的概率;
(2)若小明、小红两人都选择方案甲或都选择方案乙进行抽奖,问:他们选择何种方案抽奖,累计得分的数学期望较大?
甲、乙、丙三人进行羽毛球练习赛,其中两人比赛,另一人当裁判,每局比赛结束时,负的一方在下一局当裁判.设各局中双方获胜的概率均为 ,各局比赛的结束相互独立,第1局甲当裁判.
,各局比赛的结束相互独立,第1局甲当裁判.
(1)求第4局甲当裁判的概率;
(2)X表示前4局中乙当裁判的次数,求X的数学期望.