已知椭圆 的左右焦点分别为
的左右焦点分别为 ,点
,点 为短轴的一个端点,
为短轴的一个端点, .
.
(1)求椭圆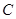 的方程;
的方程;
(2)如图,过右焦点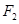 ,且斜率为
,且斜率为 的直线
的直线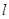 与椭圆
与椭圆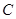 相交于
相交于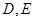 两点,
两点,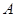 为椭圆的右顶点,直线
为椭圆的右顶点,直线 分别交直线
分别交直线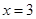 于点
于点 ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为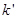 .求证:
.求证: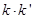 为定值.
为定值.
经过点 作直线l,若直线l与连接
作直线l,若直线l与连接 的线段总有公共点.
的线段总有公共点.
(1)求直线l斜率k的范围;
(2)直线l倾斜角 的范围;
的范围;
.已知 为常数,
为常数,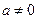 ,函数
,函数 ,
,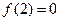 且方程
且方程 有等根.
有等根.
(1)求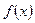 的解析式及值域;
的解析式及值域;
(2)设集合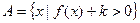 ,
,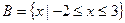 ,若
,若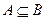 ,求实数
,求实数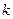 的取值范围;
的取值范围;
(3)是否存在实数 ,使
,使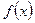 的定义域和值域分别为
的定义域和值域分别为 和
和 ?若存在,求出
?若存在,求出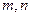 的值;若不存在,说明理由.
的值;若不存在,说明理由.
在平面直角坐标系上,设不等式组 所表示的平面区域为
所表示的平面区域为 ,记
,记 内的整点(即横坐标和纵坐标均为整数的点)的个数为
内的整点(即横坐标和纵坐标均为整数的点)的个数为
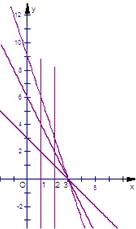
(1)求 ;并求数列
;并求数列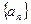 的通项公式
的通项公式 ;
;
(2)数列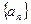 的和前
的和前 项为
项为 ,求数列
,求数列 的前n项和;
的前n项和;
(3)设 ,数列
,数列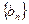 的和前
的和前 项为
项为 ,求证:
,求证: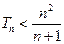
已知数列 是等差数列,
是等差数列,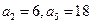 ;数列
;数列 的前n项和是
的前n项和是 ,且
,且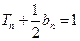 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求证:数列 是等比数列;
是等比数列;
(3)记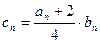 ,求
,求 的前n项和
的前n项和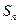
某厂用甲、乙两种原料生产A、B两种产品,已知生产1吨A产品,1吨B产品分别需要的甲、乙原料数,可获得的利润数及该厂现有原料数如下表所示.问:在现有原料下,A、B产品应各生产多少才能使利润总额最大?利润总额最大是多少?列产品和原料关系表如下:

|
A产品 (1吨) |
B产品 (1吨) |
总原料 (吨) |
||
| 甲原料(吨) |
2 |
5 |
10 |
||
| 乙原料(吨) |
6 |
3 |
18 |
||
| 利润(万元) |
4 |
3 |