点 是矩形
是矩形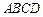 所在平面外一点,且
所在平面外一点,且 面
面 分别是
分别是 上的点,
上的点, 分
分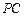 成定比2,
成定比2,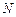 分
分 成定比1,求满足
成定比1,求满足 的实数
的实数 的值.
的值.
已知函数 若 在 上的最大值和最小值分别记为 ,
(1)求
;
(2)设
若
对
恒成立,求
取值范围.
如图,设椭圆
,动直线
与椭圆
只有一个公共点
,且点
在第一象限.
(1)已知直线
的斜率为
,用
表示点
的坐标;
(2)若过原点
的直线
与
垂直,证明:点
到直线
的距离的最大值为
.
如图,在四棱锥 中,平面 , , , . .
(1)证明:
;
(2)求二面角
的大小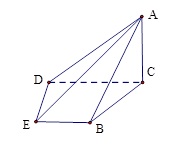
已知数列 和 满足 .若 为等比数列,且
(1)求
与
;
(2)设
。记数列
的前
项和为
.
(i)求
;
(ii)求正整数
,使得对任意
,均有
.
在 中,内角 所对的边分别为 .已知 .
(1)求角
的大小;
(2)若
,求
的面积.