.(本小题满分12分)已知双曲线的两个焦点的坐标为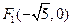 、
、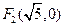 ,离心率
,离心率 .(1)求双曲线的标准方程;(2)设
.(1)求双曲线的标准方程;(2)设 是(1)中所求双曲线上任意一点,过点
是(1)中所求双曲线上任意一点,过点 的直线与两渐近线
的直线与两渐近线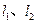 分别交于点
分别交于点 ,若
,若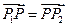 ,求
,求 的面积.
的面积.
等腰三角形的两个角的比为2 :3,试求此三角形的顶角与底角的弧度数.
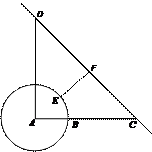
如图某粮食储备库占地呈圆域形状,它的斜对面有一条公路,从储备库中心A向正东方向走1km是储备库边界上的点B,接着向正东方向再走2km到达公路上的点C;从A向正北方向走2.8km到达公路上的另一点D,现准备在储备库的边界上选一点E,修建一条由E通往公路CD的专用(线)路EF,要求EF最短,问点E应选在何处?
 |
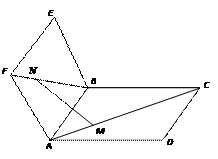
已知正方形ABCD和正方形ABEF所在的平面相交于AB,点M,N分别在AC和BF上,且AM=FN.
求证:MN‖平面BCE.
 |
一个用鲜花做成的花柱,它的下面是一个直径为2m、高为4m的圆柱形物体,上面是一个半球形体,如果每平方米大约需要鲜花200朵,那么装饰这个花柱大约需要多少朵鲜花( 取3.1)?
取3.1)?
在数列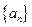 中,已知
中,已知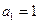 ,
,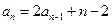 ,
,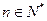 .
.
(1)求证:数列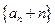 是等比数列;
是等比数列;
(2) 求数列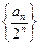 的前项和为
的前项和为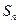 .
.