长方体ABCD—A1B1C1D1(如右图所示),宽、长、高分别为3、4、5,现有一甲壳虫从A出发沿长方体表面爬行到C1来获取食物,试画出它的最短爬行路线,并求其路程的最小值.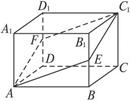
已知向量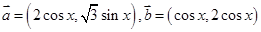 ,函数
,函数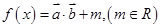 ,且当
,且当 时,
时,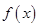 的最小值为2
的最小值为2
(Ⅰ)求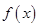 的单调递增区间;
的单调递增区间;
(Ⅱ)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的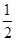 ,再把所得的图象向右平移
,再把所得的图象向右平移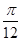 个单位,得到函数
个单位,得到函数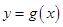 的图象,求方程
的图象,求方程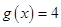 在区间
在区间 上所有根之和.
上所有根之和.
设函数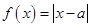
(Ⅰ)当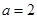 时,解不等式
时,解不等式 ;
;
(Ⅱ)若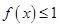 的解集为
的解集为 ,
, 求证:
求证:
已知圆 的参数方程是
的参数方程是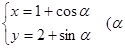 为参数).
为参数).
(Ⅰ)以直角坐标系的原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线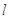 的极坐标方程为
的极坐标方程为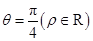 ,设直线
,设直线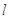 和圆
和圆 的交点为
的交点为 ,求
,求 的面积.
的面积.
设函数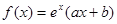 .若曲线在点
.若曲线在点 处的切线方程为
处的切线方程为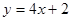 .
.
(Ⅰ)求 、
、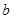 的值;
的值;
(Ⅱ)设 ,若
,若
 -2时,
-2时, ,求
,求 的取值范围.
的取值范围.
已知椭圆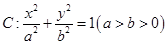 的焦点为
的焦点为 ,点
,点 在C上,且
在C上,且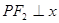 轴.
轴.
(Ⅰ)求椭圆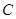 的方程;
的方程;
(Ⅱ) 若直线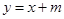 与椭圆
与椭圆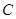 交于不同的两点
交于不同的两点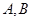 ,原点
,原点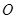 在以
在以 为直径的圆外,求
为直径的圆外,求 的取值范围.
的取值范围.