已知圆 的参数方程是
的参数方程是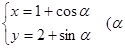 为参数).
为参数).
(Ⅰ)以直角坐标系的原点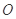 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,写出圆
轴的正半轴为极轴建立极坐标系,写出圆 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线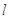 的极坐标方程为
的极坐标方程为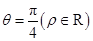 ,设直线
,设直线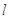 和圆
和圆 的交点为
的交点为 ,求
,求 的面积.
的面积.
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
| X |
1 |
2 |
3 |
4 |
| Y |
51 |
48 |
45 |
42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
为调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
| 性别 是否需要志愿者 |
男 |
女 |
| 需要 |
40 |
30 |
| 不需要 |
160 |
270 |
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关?
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由.
北京市2013年4月1日-4月30日对空气污染指数的监测数据如下(主要污染物为可吸入颗粒物):
61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,81,83,82,82,64,79,86,85,75,71,49,45.
(1)完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优;在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.
请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
在育民中学举行的电脑知识竞赛中,将高一两个班参赛学生的成绩(得分的整数)进行整理后分成五组,绘制出如下的频率分布直方图(如图),已知图中从左到右的第一、第二、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05第二小组的频数为40.
(1)求第二小组的频率,并补全这个频率分布直方图;
(2)求这两个班参赛的学生人数.
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图所示.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差;
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高176cm的同学被抽中的概率.