已知向量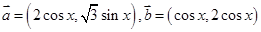 ,函数
,函数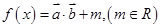 ,且当
,且当 时,
时,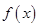 的最小值为2
的最小值为2
(Ⅰ)求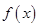 的单调递增区间;
的单调递增区间;
(Ⅱ)先将函数 的图象上的点纵坐标不变,横坐标缩小到原来的
的图象上的点纵坐标不变,横坐标缩小到原来的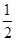 ,再把所得的图象向右平移
,再把所得的图象向右平移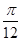 个单位,得到函数
个单位,得到函数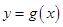 的图象,求方程
的图象,求方程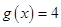 在区间
在区间 上所有根之和.
上所有根之和.
设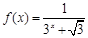 ,(1)分别求
,(1)分别求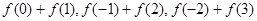 ;(2)然后归纳猜想一般性结论,并给出证明.
;(2)然后归纳猜想一般性结论,并给出证明.
已知复数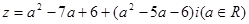 ,求a分别为何值时,
,求a分别为何值时,
(1)z是实数;(2)z是纯虚数;(3)当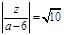 时,求Z的共轭复数.
时,求Z的共轭复数.
若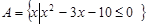 ,
,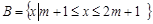
(1)当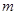 =1时,求
=1时,求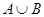
(2)若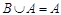 ,求
,求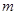 的取值范围.
的取值范围.
如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.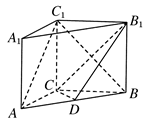
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1;
(3)求异面直线AC1与B1C所成角的余弦值.
如图所示,已知在圆锥SO中,底面半径r=1,母线长l=4,M为母线SA上的一个点,且SM=x,从点M拉一根绳子,围绕圆锥侧面转到点A,求: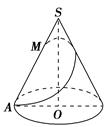
(1)设f(x)为绳子最短长度的平方,求f(x)表达式;
(2)绳子最短时,顶点到绳子的最短距离;
(3)f(x)的最大值.