某社团组织20名志愿者利用周末和节假日参加社会公益活动,志愿者中,年龄在20至40岁的有12人,年龄大于40岁的有8人.
(1)在志愿者中用分层抽样方法随机抽取5名,年龄大于40岁的应该抽取几名?
(2)上述抽取的5名志愿者中任取2名,求取出的2人中恰有1人年龄大于40岁的概率.
已知函数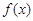 的定义域为
的定义域为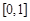 ,且
,且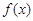 的图象连续不间断. 若函数
的图象连续不间断. 若函数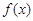 满足:对于给定的
满足:对于给定的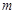 (
(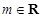 且
且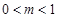 ),存在
),存在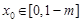 ,使得
,使得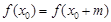 ,则称
,则称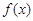 具有性质
具有性质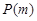 .
.
(1)已知函数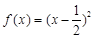 ,
,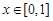 ,判断
,判断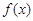 是否具有性质
是否具有性质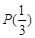 ,并说明理由;
,并说明理由;
(2)已知函数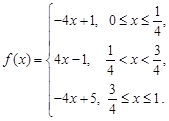 若
若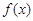 具有性质
具有性质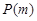 ,求
,求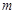 的最大值;
的最大值;
(3)若函数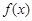 的定义域为
的定义域为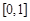 ,且
,且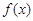 的图象连续不间断,又满足
的图象连续不间断,又满足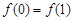 ,
,
求证:对任意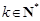 且
且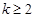 ,函数
,函数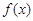 具有性质
具有性质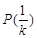 .
.
已知点 ,点
,点 为直线
为直线 上的一个动点.
上的一个动点.
(1)求证: 恒为锐角;
恒为锐角;
(2)若四边形 为菱形,求
为菱形,求 的值.
的值.
已知函数 .
.
(1)请用“五点法”画出函数 在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);
在长度为一个周期的闭区间上的简图(先在所给的表格中填上所需的数值,再画图);

(2)求函数 的单调递增区间;
的单调递增区间;
(3)当 时,求函数
时,求函数 的最大值和最小值及相应的
的最大值和最小值及相应的 的值.
的值.
已知函数 ,其中
,其中 为常数.
为常数.
(1)若函数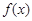 在区间
在区间 上单调,求
上单调,求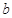 的取值范围;
的取值范围;
(2)若对任意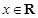 ,都有
,都有 成立,且函数
成立,且函数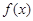 的图象经过点
的图象经过点 ,
,
求 的值.
的值.