如图,在三棱柱 中,点
中,点 分别是
分别是 的中点,
的中点, 为
为 的重心,取
的重心,取 三点中的一点作为点
三点中的一点作为点 ,是否存在一点,使得三棱柱恰有2条棱和平面
,是否存在一点,使得三棱柱恰有2条棱和平面 平行,若存在,写出这个点;若不存在,说明理由.
平行,若存在,写出这个点;若不存在,说明理由. 
(本小题满分12分)
已知△ABC的面积为3,且满足 ,设
,设 和
和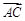 的夹角是
的夹角是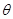 ,
,
(1)求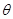 的取值范围;
的取值范围;
(2)求函数 的最大值。
的最大值。
已知函数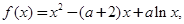 其中常数
其中常数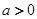
(Ⅰ)当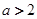 时,求函数
时,求函数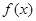 的单调递增区间;
的单调递增区间;
(Ⅱ) 当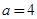 时,若函数
时,若函数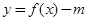 有三个不同的零点,求m的取值范围;
有三个不同的零点,求m的取值范围;
(Ⅲ)设定义在D上的函数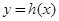 在点
在点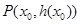 处的切线方程为
处的切线方程为 当
当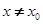 时,若
时,若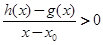 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数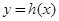 的“类对称点”,请你探究当
的“类对称点”,请你探究当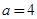 时,函数
时,函数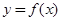 是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标,若不存在,说明理由。
是否存在“类对称点”,若存在,请最少求出一个“类对称点”的横坐标,若不存在,说明理由。
.
已知圆M: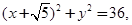 定点
定点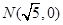 ,点
,点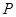 为圆
为圆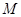 上的动点,点
上的动点,点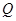 在
在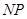 上,点
上,点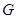 在
在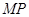 上,且满足
上,且满足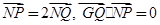 。
。
(Ⅰ) 求点G的轨迹C的方程;
(Ⅱ) 过点(2,0)作直线l,与曲线C交于A,B两点,O是坐标原点,设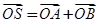 ,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。
,是否存在这样的直线l,使四边形OASB的对角线相等(即|OS|=|AB|)?若存在,求出直线l的方程;若不存在,试说明理由。
本题满分14分)
在数列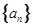 中,
中, ,且
,且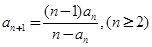 .
.
(Ⅰ) 求 ,猜想
,猜想 的表达式,并加以证明;
的表达式,并加以证明;
(Ⅱ) 设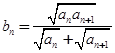 ,求证:对任意的自然数
,求证:对任意的自然数 ,都有
,都有 ;
;
某学校某班文娱小组的每位组员唱歌、跳舞至少会一项,已知已知会唱歌的有2人,会跳舞听有5人,现从中选2人。设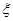 为选出的人中既会唱歌又会跳舞的人数,且
为选出的人中既会唱歌又会跳舞的人数,且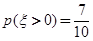 。
。
(1)请你判断该班文娱小组的人数并说明理由;
(2)求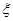 的分布列与数学期望。
的分布列与数学期望。